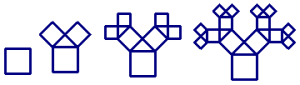
Napíšte rekurzívnu procedúru, pomocou ktorej sa vykreslí "Pytagorov strom" podľa predlohy na obrázku, do zvoleného stupňa.

1. Ako z predchádzajúcich príkladov môžme povedať, že procedúra bude mať dva parametre, jeden dĺžku strany a druhý stupeň krivky. Podľa obrázka vieme, že ak je stupeň=0, tak sa nakreslí iba štvorec. Zatiaľ procedúra bude vyzerať takto:

   viem pyt :a :n
   	ak :n=0
   	[	opakuj 4
   		[ do :a vl 90 ]
   	]
   koniec

   
   
2. Z obrázka vidíme, že trojuholník nad štvorcom je rovnoramenný a pravouhlý. Podľa Pytagorovej vety si vieme vypočítať dĺžku odvesny. Táto odvesna je zároveň aj stranou menšieho štvorca. Z Pytagorovej vety dostaneme, že odvesna má dĺžku a/sqrt(2). Ďalej vieme, že trojuholník je rovnoramenný, takže uhly pri základní sú 45°.

    

3. Ideme kresliť krivku stupňa 1. Je tam štvorec, trojuholník a dva malé štvorce, ktoré sú spojené jedným bodom. Ako vidíme, trojuholník je vytvorený zo strán menších štvorcov a väčšieho. Takže nemusíme kresliť aj trojuholník, ten vznikne nakreslením troch štvorcom, z ktorých každé dva majú spoločný jeden vrchol.

   Nakreslíme štvorec (väčší), prejdeme stranu toho štvorca, otočíme sa o 45° doprava a tam by sme mali nakresliť ďalší menší štvorec:

   viem pyt :a :n
   	ak2 :n=0
   	[
   		opakuj 4 [do :a vl 90 ]
   	]
   	[
   		opakuj 4 [do :a vl 90 ]
   		do :a
   		vp 45
   		...
   	]
   koniec

   
   
4. Potrebujeme kresliť menší štvorec. Vieme však, že ak zavoláme tú istú procedúru so zníženým stupňom, tak sa nakreslí len štvorec. Takže zavoláme procedúru pyt s hodnotami a=a/sqrt(2) a stupeň=stupeň-1. Po tomto sa potrebujeme otočiť, aby sme prešli po odvesne a začali kresliť druhý štvorec. Otočenie bude o 90° a prejdeme už známu dĺžku a/sqrt(2) . Rovno, tak ako sme natočení môžme kresliť druhý štvorec, takisto zavolaním procedúry pyt s rovnakými parametrami ako v predchádzajúcom volaní. Teda upravená procedúra je:
   
   

   viem pyt :a :n
   	ak2 :n=0
   	[ opakuj 4 [do :a vl 90 ] ]
   	[
   		opakuj 4 [do :a vl 90 ]
   		do :a vp 45
   		pyt :a/sqrt(2) :n-1
   		vl 90
   		do :a/sqrt(2)
   		pyt :a/sqrt(2) :n-1
   		. . .
   	]
   koniec

   
   
5. Teraz už máme nakreslené všetky tri štvorce a potrebujeme sa vrátiť na miesto z ktorého sme začínali. Teda ešte sa otočíme do ľava o 90°, prejdeme dĺžku odvesny a po obvode prejdeme väčší štvorec až namiesto, odkiaľ sme začínali. Procedúra vyzerá takto:
   
   
   

   viem pyt :a :n
   	ak2 :n=0
   	[ opakuj 4 [do :a vl 90 ] ]
   	[
   		opakuj 4 [do :a vl 90 ]
   		do :a vp 45
   		pyt :a/sqrt(2) :n-1
   		vl 90
   		do :a/sqrt(2)
   		pyt :a/sqrt(2) :n-1
   		vl 90
   		do :a/sqrt(2) vl 45
   		do :avl 90
   		do :a vl 90
   	]
   koniec

   
   

Procedúru môžme zavolať príkazom pyt 80 5

Ak nie je vidieť Imagine projekt, treba stiahnuť Imagine plugin