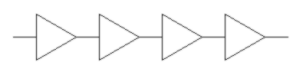
Napíšte rekurzívny podprogram, ktorý nakreslí obrázok podľa zadaného stupňa (ak sa zadá 1 tak sa nakreslí len čiara, ak 2 tak sa nakreslí čiara a trojuholník, atď.).

Riešenie:

1. Ako už vieme, tak pri nepriamej rekurzii musíme zistiť z koľkých rôznych častí sa skladá výstup (to čo máme nakresliť). Keďže máme nakresliť čiaru, ktorá sa skladá z čiary a trojuholníka, tak máme dve rôzne časti a to čiaru a trojuholník.
   Procedúra pre čiaru bude vyzerať tak ako v predchádzajúcom príklade:
   
   

   viem CIARA
   	do 40
   koniec

   
   a procedúra pre trojuholník bude vyzerať takto:
   
   

   viem TROJUHOLNIK
   	do 80 vl 120
   	do 80 vl 120
   	do 80 vl 120
   koniec

   
   Takáto procedúra nám síce nakresli trojuholník, ale my tento trojuholník potrebujeme napojiť na predtým nakreslenú čiaru. Trojuholník musíme začať kresliť z prostriedku jednej strany, teda:
   
   

   viem TROJUHOLNIK
   	vp 90
   	do 40
   	vl 120 do 80
   	vl 120 do 80
   	vl 120
   	do 40
   koniec

   
   Táto procedúra nám už bude kresliť trojuholník z miesta, kde je koniec predtým nakreslenej čiary. Potrebujeme ešte upraviť procedúru TROJUHOLNÍK tak, aby po skončení kreslenia trojuholníka bolo možné zase nakresliť čiaru. Upravíme ju tak, že po skončení nakreslenia trojuholníka sa otočíme a premiestnime do protiľahlého vrcholu trojuholníka (musíme prejsť dĺžku rovná výške tohto trojuholníka). To akú dĺžku musíme prejsť si vypočítame pomocou Pytagorovej vety (nesmieme pri premiestňovaní zabudnúť zdvihnúť pero, aby sme za sebou nerobili čiaru a potom po premiestnení zase pero položiť dole). Upravená procedúra vyzerá takto:
   

   viem TROJUHOLNIK
   	vp 90
   	do 40 vl 120
   	do 80 vl 120
   	do 80 vl 120
   	do 40
   	vp 90
   	ph
   	do sqrt(60*60-30*30)
   	pd
   koniec

   
   
2. Už máme procedúry, ktoré vykreslia jednotlivé časti. Musíme určiť, kde bude rekurzívne volanie v procedúre na druhú procedúru. Najprv sa musí nakresliť čiara a až potom zavolať procedúra TROJUHOLNIK a v druhej procedúre sa najprv musí nakresliť trojuholník a až potom zavolať procedúra. Rekurzívne volanie a inú procedúru bude za príkazmi nakreslenia príslušného útvaru.
   
   

   viem CIARA do 40 TROJUHOLNIK koniec

   viem TROJUHOLNIK vp 90 do 40 vl 120 do 80 vl 120 do 80 vl 120 do 40 vp 90 ph do sqrt(60*60-30*30) pd CIARA koniec

   
   
3. Takto napísané procedúry sa budú volať donekonečna. Keďže máme vykresliť čiaru podľa zadaného stupňa, tak parameter procedúr bude stupeň čiary, ktorú máme vykresliť. A už z predchádzajúceho príkladu vieme že hodnota parametra sa musí nejako meniť (pretože máme vykresliť čiaru s toľkých častí aký je zadaný stupeň). Po nakreslení časti čiary sa nám už stupeň zníži o jeden, teda pri volaní druhej procedúry znížime hodnotu parametra (ktorý sme malý ak vstupný) o jednotku.
   

   viem CIARA :n do 40 TROJUHOLNIK :n-1 koniec

   viem TROJUHOLNIK :a vp 90 do 40 vl 120 do 80 vl 120 do 80 vl 120 do 40 vp 90 ph do sqrt(60*60-30*30) pd CIARA :a-1 koniec

   
   
4. Máme už určené to, ako budú vyzerať jednotlivé procedúry. Potrebujeme ešte napísať podmienku pre ukončenie rekurzívneho volania procedúr. Ako parameter máme stupeň čiary a ten sa nám v rekurzívnom volaní stále znižuje. Stupeň sa môže znižovať len po hodnotu 0 (čiaru so záporným stupňom nevieme nakresliť), takže podmienka ukončenia rekurzívneho volania bude závisieť od hodnoty parametra. Ak parameter bude mať hodnotu nula alebo zápornú, tak sa nemusí nič vykonávať, ak má parameter hodnotu väčšiu ako 0, tak sa môžu funkcie rekurzívne volať (do času pokiaľ parameter nebude nula).
   

   viem CIARA :n ak :n>0 [ do 40 TROJUHOLNIK :n-1 ] koniec

   viem TROJUHOLNIK :a ak :a>0 [ vp 90 do 40 vl 120 do 80 vl 120 do 80 vl 120 do 40 vp 90 ph do sqrt(80*80-40*40) pd CIARA :a-1 ] koniec

Aby sme nakreslili čiaru, tak zavoláme procedúru čiara, napríklad takto CIARA 5

Ak nie je vidieť Imagine projekt, treba stiahnuť Imagine plugin