PALMA junior
Úloha o kruhovej čipke

Autorské riešenie
[stiahni py, py, py, py]

• Počet riešiteľov: 33 / 45 =  73,3 %

• Úspešnosť riešenia: 3.4 / 6 = 56,6 %

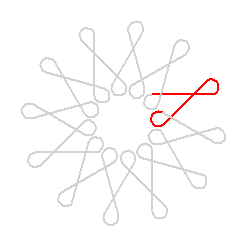
Podľa zadania úlohy máme vytvoriť funkciu na vykreslenie kruhovej čipky. Na obrázku nižšie je znázornená kruhová čipka s 12 oblúkmi, v ktorom sme našli a červenou farbou zvýraznili vzor, ktorý sa 12-krát opakuje. Tento vzor je tvorený 4 časťami: úsečkou, ľavotočivým kružnicovým oblúkom, úsečkou, pravotočivým kružnicovým oblúkom.

Aby sme vedeli vykresliť túto kruhovú čipku, potrebujeme vypočítať patričné uhly pri ľavotočivom a pravotočivom kružnicovom oblúku. Veľmi užitočnou stratégiou pri riešení tohto problému je vyriešenie jednoduchšieho problému, v ktorom vykresľujeme lineárnu čipku s rovnakým opakujúcim sa vzorom.  

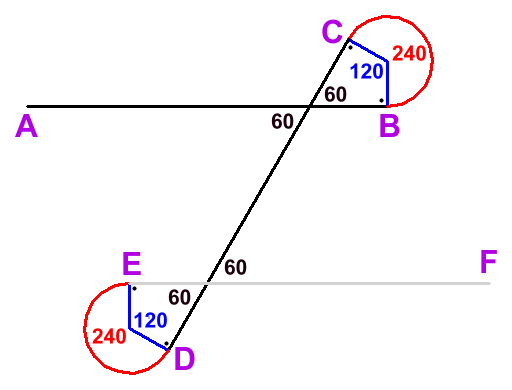
Pozrime sa, ako by sme riešili jednoduchší problém s lineárnou čipkou. Pri nej je najdôležitejšíe vykresliť opakujúci sa vzor. Prirodzenou stratégiou riešenia je nakreslenie náčrtu vzoru, v ktorom vyznačíme patričné uhly. Opakujúci sa vzor je tvorený: úsečkou AB, ľavotočivým kružnicovým oblúkom BC, úsečkou CD, pravotočivým kružnicovým oblúkom DE

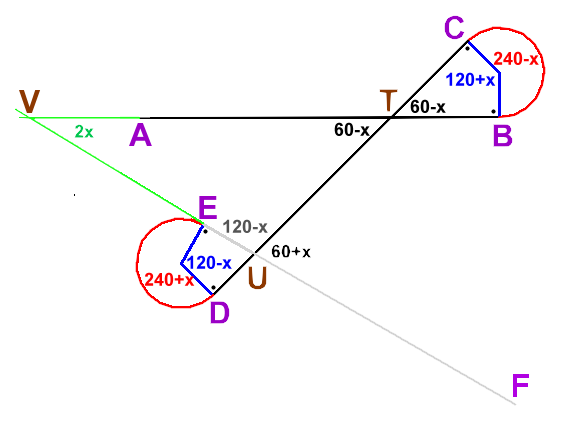
Ak si zvolíme veľkosť uhla medzi úsečkami AB a CD na napr. 60 stupňov, potom po krátkej úvahe určíme veľkosť uhla ľavotočivého kružnicového oblúka BC na 180 + 60 stupňov.  A rovnako určíme veľkosť uhla pravotočivého kružnicového oblúka DE na rovnakú hodnotu uhla 180 + 60 stupňov.

Funkcia na vykreslenie lineárnej čipky so zadanou dĺžkou úsečiek a počtom opakujúcich sa vzorov môže vyzerať napr. nasledovne:

import turtle

def kresli(dlzka, pocet):
    for _ in range(pocet):
        turtle.forward(dlzka)
        turtle.circle(dlzka / 8, 240)
        turtle.forward(dlzka)
        turtle.circle(-dlzka / 8, 240)

kresli(100, 12)
turtle.mainloop()

Tu poznamenávame, že pri vykresľovaní ľavotočivých kružnicových oblúkov pomocou metódy circle() používame kladnú hodnotu dĺžky ich polomeru, pri pravotočivých zápornú hodnotu. 

Pozrime sa teraz na to, ako vyriešiť pôvodný problém (vykresľovanie kruhovej čipky) pomocou riešenia jednoduchšieho problému (vykresľovanie lineárnej čipky). Oproti riešeniu vykresľovania lineárnej čipky, v riešení vykresľovania kruhovej čipky potrebujeme  zmeniť už len uhly pri vykresľovaní ľavotočivého BC a pravotočivého DE kružnicového obluka.

Jednou z možností je zmenšiť veľkosť kružnicového oblúka BC z hodnoty 240 na hodnotu 240 - x a zároveň zväčšiť veľkosť kružnicového oblúka DE z hodnoty 240 na hodnotu 240 + x. Z náčrtu nižšie môžeme jednoducho odvodiť hodnotu x nasledovne. Z trojuholníka TVU sa dá určiť uhol TVU = 2x, veľkosť uhla TVU = veľkosti uhla BVE, ktorá je uhlom natočenia pri vykresľovaní nasledovného vzoru. Podľa zadaného poštu vzorov sa dá uviesť 2x = 360 / počet a z toho x = 180 / počet. Takto dostaneme pre ľavotočivý kružnicový oblúk veľkosť uhla 240 - 180 / počet a pre pravotočivý kružnicový oblúk veľkosť uhla 240 + 180 / počet.   

Funkcia kresli na vykreslenie kruhovej čipky so zadanou veľkosťou úsečiek a zadaným počtom opakujúcich sa vzorov môže vyzerať napr. nasledovne:

import turtle

def kresli(dlzka, pocet):
    for _ in range(pocet):
        turtle.forward(dlzka)
        turtle.circle(dlzka / 8, 240 - 180 / pocet)
        turtle.forward(dlzka)
        turtle.circle(-dlzka / 8, 240 + 180 / pocet)

kresli(100, 24)
turtle.mainloop()

Alternatívnym riešením je ponechanie veľkosti uhla ľavotočivého kružnicového oblúka na hodnote 240 a zmena veľkosti uhla pravotočivého kružnicového oblúka na hodnotu 240 + 360 / počet. Funkcia kresli pre tento alternatívny prístup môže vyzerať napr. nasledovne:

import turtle

def kresli(dlzka, pocet):
    for _ in range(pocet):
        turtle.forward(dlzka)
        turtle.circle(dlzka / 8, 240)
        turtle.forward(dlzka)
        turtle.circle(-dlzka / 8, 240 + 360 / pocet)

kresli(100, 24)
turtle.mainloop()

Ďalším alternatívnym riešením je zmena veľkosti uhla ľavotočivého kružnicového oblúka na hodnotu 240 - 360 / počet a ponechanie veľkosti uhla pravotočivého kružnicového oblúka na hodnote 240. Funkcia kresli pre tento alternatívny prístup môže vyzerať napr. nasledovne:

import turtle

def kresli(dlzka, pocet):
    for _ in range(pocet):
        turtle.forward(dlzka)
        turtle.circle(dlzka / 8, 240 - 360 / pocet)
        turtle.forward(dlzka)
        turtle.circle(-dlzka / 8, 240)

kresli(100, 24)
turtle.mainloop()

Nad rámec zadania tejto úlohy môžeme dospieť k zovšeobecneniu uvedených 3 riešení, kde funkcia kresli bude mať až 5 parametrov: dĺžku úsečky, počet oblúkov čipky po jej obvode, veľkosť uhla medzi susednými úsečkami, pomer polomeru oblúka a dĺžky úsečky, pomocný uhol určujúci natočenie ľavotočivého (a následne aj pravotočivého) kružnicového oblúka. Funkcia kresli pre toto zovšeobecnené riešenie vykresľovania kruhovej čipky môže vyzerať napr. nasledovne:

import turtle

def kresli(dlzka, pocet, uhol, koeficient, uhol2):
    for _ in range(pocet):
        turtle.forward(dlzka)
        turtle.circle(dlzka * koeficient, 180 + uhol - uhol2 / pocet)
        turtle.forward(dlzka)
        turtle.circle(-dlzka * koeficient, 180 + uhol + (360 - uhol2) / pocet)

kresli(100, 24, 60, 0.125, 180)
turtle.mainloop()

Táto úloha je zameraná na:

• použitie stratégií riešenia problémov - zjednodušenie zadania, hľadanie vzoru, nakreslenie obrázku, dekompozíciu problému.

• precvičenie príkazov volania funkcií s parametrami, cyklu for, príkazov korytnačej grafiky, tvorby aritmetických výrazov.

Vaše zaujímavé riešenia a najčastejšie chyby

Do riešenia úlohy sa zapojilo 10 tímov z kategórie EXPERT a 23 tímov z kategórie GURU. Plný počet bodov za svoje riešenie získalo až 10 tímov: karborura, emily a emka, gumy, jama, none of the above, o(n!), qwerty, raketak, the bug slayers a vevericky, ktorým srdečne gratulujeme.

V riešeniach sme zaregistrovali nasledovné nedostatky, vychádzajúce najčastejšie z nedôslednej analýzy problému:

• vyriešenie úlohy len pre konkrétny ilustračný príklad bez zovšeobecnenia,

• vykreslenie neuzavretej čipky úplne zlým výpočtom, resp. zbytočným použitím funkcie int,

• vykreslenie podobnej alebo inej čipky, ktorá sa odlišovala od požadovanej čipky zo zadania,

• nesprávne zredukovanie riešenia problému len na jeden parameter,

•  použitie viacerých nerelevantných parametrov,

• použitie funkcie bez parametrov,

• nepoužitie funkcie,

• pri vykresľovaní použitie len kružnicových oblúkov bez úsečiek, ktoré boli požadované v zadaní,

• neefektívne použitie cyklov pri vykresľovaní kružnicových oblúkov namiesto metódy circle,

• konštantné polomery oblúkov, podľa zadania mali byť odvodené od dĺžky úsečiek.