PALMA junior
Úloha o optimálnom mieste

Autorské riešenie
[stiahni balikobox.py]

• Počet riešiteľov: 24 /  =  %

• Úspešnosť riešenia: 3,85 / 7 = 55 %

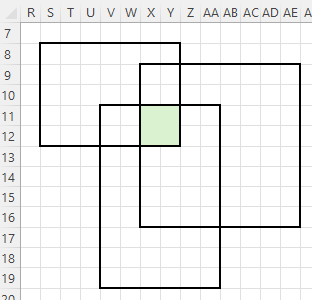
V tejto úlohe musíme vyriešiť problém, či niekoľko zadaných obdĺžnikov má spoločný prienik. Pozrime sa najskôr ako zistiť, či takýto prienik existuje.

Preskúmajme nasledujúci príklad:

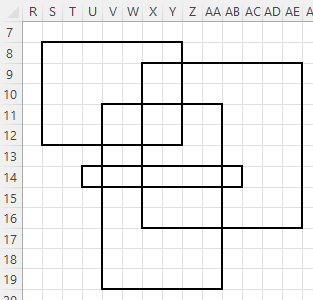
Ak prienik existuje, zrejme to bude tiež nejaký obdĺžnik. Zistime najskôr, aké budú súradnice jeho stĺpcov a potom súradnice jeho riadkov.

Z obrázka vyššie môžeme zovšeobecniť. Ľavá súradnica stĺpca prienikového obdĺžnika musí byť väčšia alebo rovná ako je najväčšia ľavá súradnica stĺpcov všetkých obdĺžnikov. Na obrázku vyššie je to max('S', 'V', 'X') = 'X'. Podobne pre pravú súradnicu stĺpca prienikového obdĺžnika platí, že musí byť menšia alebo rovná ako najmenšia pravá súradnica stĺpcov všetkých obdĺžnikov. Na obrázku vyššie je to min(Y', 'AA', 'AE') = 'X'. Vieme teda, že prienikový obdĺžnik sa nachádza niekde medzi stĺpcami 'X' ... 'Y'.

Podobnú úvahu vieme aplikovať pre riadky prienikového obdĺžnika. Jeho riadok musí byť aspoň max(8, 9, 11) = 11 a najviac min(12, 16, 19) = 12. Nachádza sa teda niekde medzi riadkami 11 .. 12.

Vidíme, že  tomto prípade takýto obdĺžnik existuje: ['X', 11, 'Y', 12]. Samozrejme ho môžeme určiť aj inou dvojicou protiľahlých vrcholov, napr.: ['Y', 11, 'X', 12].

Pozrime sa, ako to dopadne, ak takýto prienikový obdĺžnik neexistuje:

Ak by sme chceli nájsť prienikový obdĺžnik v tomto prípade, tak:

Jeho stĺpce by mali byť medzi: max('S', 'U' 'V', 'X') = 'X' a min('Y', 'AA', 'AB', 'AE') = 'Y'.

Jeho riadky by mali byť medzi: max(8, 9, 11, 14) = 14 a min(12, 14, 16, 19) = 12.

Vidíme, že takýto obdĺžnik neexistuje. Najmenšie z čísiel jeho riadkov (14) by malo byť menšie alebo rovné ako najväčšie z čísiel jeho riadkov (12), čo ale neplatí 14 > 12.

Zhrňme si to. Ak platí:

• max(ľavé stĺpce obdĺžnikov) <= min(pravé stĺpce obdĺžnikov)
  
  a

• max(horné riadky obdĺžnikov) <= min(spodné riadky obdĺžnikov)

tak prienikový obdĺžnik existuje. V opačnom prípade neexistuje.

Obdĺžniky môžu byť zadané ľubovoľnou dvojicou protiľahlých vrcholov. Ďalšou otázkou je, ako zistiť ktorý stĺpec je ľavý a ktorý pravý a ako zistiť, ktorý riadok je horný a ktorý spodný?

Stačí ich porovnať. Pre obdĺžnik [stĺpec1, riadok1, stĺpec2, riadok2] platí:

• ľavý stĺpec = min(stĺpec1,stlípec2)

• pravý stĺpec = max(stĺpec1,stlípec2)

• horný riadok = min(riadok1, riadok2)

• spodný riadok = max(riadok1, riadok2) 

Zatiaľ, čo riadky sa dajú porovnať prirodzene, pri stĺpcoch to je o niečo komplikovanejšie.

Nemôžeme ich porovnávať abecedne^(*). Napr.  'AB' < 'Z' ale stĺpec 'AB' je až za stĺpcom 'Z'.

Abecedné porovnanie by platilo len v prípade, že ich názvy sú rovnako dlhé. Ak názvy stĺpcov nie sú rovnako dlhé, tak stĺpec s kratším menom je určite pred stĺpcom s dlhším menom. 

Ak teda porovnávame stĺpce, najskôr porovnajme dĺžky ich názvov. Ak sú dĺžky rovnaké, porovnajme ich abecedne.

Ak všetky predchádzajúce úvahy spojíme, tak výsledný program môže vyzerať nasledovne:

def kluc_stlpec(stlpec):
    return len(stlpec), stlpec

def existuje_miesto(poziadavky):
    stlpec1, riadok1, stlpec2, riadok2 = poziadavky[0]

    stlpec_lavy = min(stlpec1, stlpec2, key=kluc_stlpec)
    stlpec_pravy = max(stlpec1, stlpec2, key=kluc_stlpec)
    riadok_horny = min(riadok1, riadok2)
    riadok_spodny = max(riadok1, riadok2)

    for poziadavka in poziadavky:
        stlpec1, riadok1, stlpec2, riadok2 = poziadavka
        stlpec_lavy = max(stlpec_lavy,
                          min(stlpec1, stlpec2, key=kluc_stlpec), key=kluc_stlpec)
        stlpec_pravy = min(stlpec_pravy,
                           max(stlpec1, stlpec2, key=kluc_stlpec), key=kluc_stlpec)
        riadok_horny = max(riadok_horny,
                           min(riadok1, riadok2))
        riadok_spodny = min(riadok_spodny,
                            max(riadok1, riadok2))
    return kluc_stlpec(stlpec_lavy) <= kluc_stlpec(stlpec_pravy)\
           and\
           riadok_horny <= riadok_spodny

Všimnime si funkciu kluc_stlpec. Pomocou nej vyriešime porovnávanie stĺpcov. Táto funkcia pre zadaný názov stĺpca vráti dvojicu: dĺžka názvu stĺpca a názov stĺpca. Ak takúto dvojicu využijeme pri porovnávaní stĺpcov (argument key pri funkciách min a max), tak sa stĺpce najskôr porovnajú podľa dĺžky ich názvov. Ak sú dĺžky názvov rovnaké, tak sa porovnajú abecedne.

(*) Namiesto pojmu abecedné porovnanie by sme mali správne používať pojem lexikografické porovnanie (poradie znakov v tabuľke znakov). Podľa abecedy platí 'Č' < 'Z', ale lexikograficky platí opak, 'Z' < 'Č'. Keďže názvy stĺpcov neobsahujú diakritiku, lexikografické porovnanie je v tomto prípade rovnaké ako abecedné porovnanie.

Vaše zaujímavé riešenia a najčastejšie chyby

V tejto úlohe vás potrápilo porovnávanie stĺpcov. Niektorí z vás to vyriešili tak, že hodnotu stĺpca nahradili číslom. Zápis stĺpca brali ako zápis čísla v 26-ovej sústave. Napr. "AD" = 1*26**1 + 4*26**0.

Niektorí z vás si neuvedomili, že každý obdĺžnik môže byť zadaný štyrmi rôznymi spôsobmi a predpokladali len kombináciu ľavý horný vrchol s pravým dolným vrcholom.