PALMA junior
Úloha o osemuholníkovej záhrade

Autorské riešenie
[stiahni py, py, py]

• Počet riešiteľov: 20 / 26 =  76.92 %

• Úspešnosť riešenia: 3,38 / 7 = 48.21 %

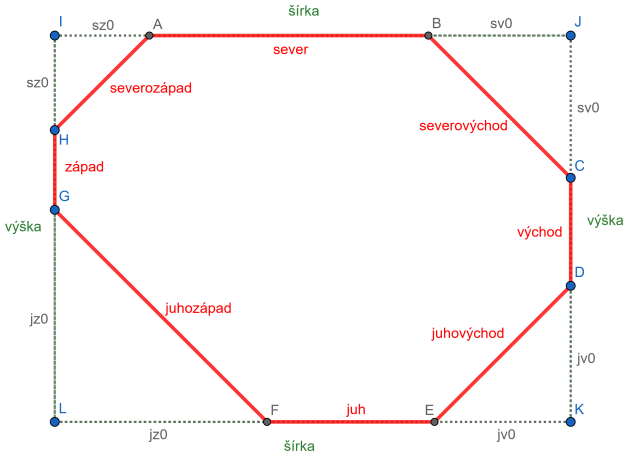
Pri jej riešení tejto grafickej úlohy si pomôžeme grafickým náčrtom nepravidelného osemuholníka s rovnakými vnútornými uhlami umiestneného v obdĺžnikovej parcele so zadanými rozmermi sirka a vyska.

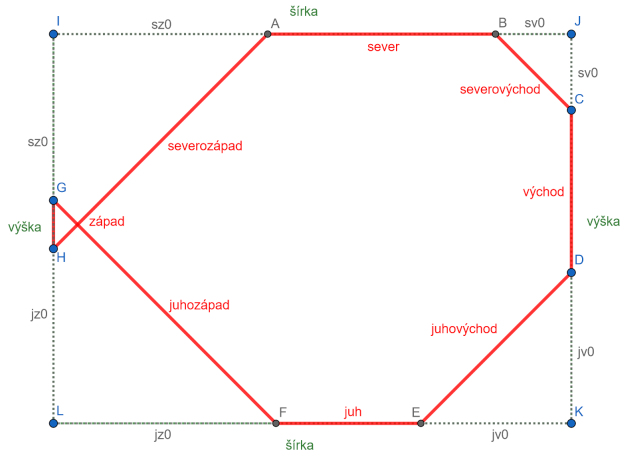
Z náčrtu môžeme odpozorovať, že nepravidelný osemuholník ABCDEFGH s rovnakými vnútornými uhlami (=135 stupňov) môžeme dostať "odrezaním" rovnoramenných pravouhlých trojuholníkov v rohoch obdĺžnikovej parcely. Pre dĺžky úsečiek osemuholníka umiestneného v obdĺžniku platí:

|IA|  +  |AB|  +  |BJ|  = sz0 + sever + sv0 = sirka

|JC|  +  |CD|  +  |DK| = sv0 + vychod + jv0 = vyska

|LG|  +  |GH|  +  |HI| = jz0 + zapad + sz0 = vyska

severozapad = √2 ∙ sz0

severovychod = √2 ∙ sv0

juhovychod = √2 ∙ jv0

juhozapad = √2 ∙ jz0

 Z uvedených vzťahov vidíme, že pri zadaných rozmeroch parcely sirka  a vyska, vieme dlžky osemuholníka vypočítať z hodnôt premenných sz0, sv0, jv0, jz0, ktoré predstavujú dĺžky "odrezkov" obdlžníka.

Hodnoty premenných c nemôžeme generovať ľubovoľne, aby sme nenastala situácia, že dostaneme niektorú z dĺžkov zápornú resp. že osemuholník nebude konvexný, ako je to uvedené na obrázku nižšie.

Na experimentovanie s generovaním náhodného osemuholníka môže poslúžiť applet v Geogebre, ktorý umožňuje meniť polohu 4 bodov osemuholníka C, D, G, H.

Pri náhodnom generovaní hodnôt premenných sz0, sv0, jv0, jz0 by sme mali zohľadniť v každom jednotlivom kroku riešiteľnosť tejto úlohy a uvažovať minimálne hodnoty možných úsekov, napr.:

sz0 = náhodné_desatinné_číslo(0, min(vyska, sirka))
sv0 = náhodné_desatinné_číslo(0, min(sirka - sz0, vyska))
jv0 = náhodné_desatinné_číslo(0, min(vyska - sv0, sirka))
jz0 = náhodné_desatinné_číslo(0, min(sirka - jv0, vyska - sz0))

Výsledný program (osemhuholnik.py) môže vyzerať napr. nasledovne:

import random


def strany_osemuholnika(sirka, vyska):
    sz0 = random.uniform(0, min(vyska, sirka))
    sv0 = random.uniform(0, min(sirka - sz0, vyska))
    jv0 = random.uniform(0, min(vyska - sv0, sirka))
    jz0 = random.uniform(0, min(sirka - jv0, vyska - sz0))
    zapad = vyska - sz0 - jz0
    vychod = vyska - sv0 - jv0
    sever = sirka - sz0 - sv0
    juh = sirka - jz0 - jv0
    severozapad = sz0 * 2 ** 0.5
    severovychod = sv0 * 2 ** 0.5
    juhovychod = jv0 * 2 ** 0.5
    juhozapad = jz0 * 2 ** 0.5
    vysledok = [sever, severovychod, vychod, juhovychod, juh, juhozapad, zapad, severozapad]
    return vysledok


print(strany_osemuholnika(400, 300))

V uvedenom riešení môže nastať situácia, že niektorá z premenných sz0, sv0, jv0, jz0 nadobudne nulovú hodnotu. Aj keď je pri generátore náhodných desatinných čísel veľmi malá šanca dosiahnúť nulovú hodnotu, ošetríme ju v programe pomocou cyklu while. Program s ošetrením kladných hodnôt dĺžok osemuholníka (osemhuholnik1.py) môže vyzerať napríklad nasledovne:

import random


def strany_osemuholnika(sirka, vyska):
    podmienka = True
    while podmienka:   
        sz0 = random.uniform(0, min(vyska, sirka))
        sv0 = random.uniform(0, min(sirka - sz0, vyska))
        jv0 = random.uniform(0, min(vyska - sv0, sirka))
        jz0 = random.uniform(0, min(sirka - jv0, vyska - sz0))
        zapad = vyska - sz0 - jz0
        vychod = vyska - sv0 - jv0
        sever = sirka - sz0 - sv0
        juh = sirka - jz0 - jv0
        severozapad = sz0 * 2 ** 0.5
        severovychod = sv0 * 2 ** 0.5
        juhovychod = jv0 * 2 ** 0.5
        juhozapad = jz0 * 2 ** 0.5
        vysledok = [sever, severovychod, vychod, juhovychod, juh, juhozapad, zapad, severozapad]
        podmienka = 0 in vysledok
    return vysledok


print(strany_osemuholnika(400, 300))

Iným riešením je zapracovanie minimálnej dĺžky strán osemuholníka odvodenej ako pomernú časť (napr. 1/20) z menšej z dĺžok parcely. Výsledný program so zapracovaním minimálnej dĺžky strán  (osemhuholnik2.py) môže vyzerať napríklad nasledovne:

import random


def strany_osemuholnika(sirka, vyska):
    min_dlzka = min(vyska, sirka) / 20
    vyska_d = vyska - min_dlzka * (2 ** 0.5 + 1)
    sirka_d = sirka - min_dlzka * (2 ** 0.5 + 1)
    sz0_d = random.uniform(0, min(vyska_d, sirka_d))
    sv0_d = random.uniform(0, min(sirka_d - sz0_d, vyska_d))
    jv0_d = random.uniform(0, min(vyska_d - sv0_d, sirka_d))
    jz0_d = random.uniform(0, min(sirka_d - jv0_d, vyska_d - sz0_d))
    zapad = vyska_d - sz0_d - jz0_d + min_dlzka
    vychod = vyska_d - sv0_d - jv0_d + min_dlzka
    sever = sirka_d - sz0_d - sv0_d + min_dlzka
    juh = sirka_d - jz0_d - jv0_d + min_dlzka
    severozapad = sz0_d * 2 ** 0.5 + min_dlzka
    severovychod = sv0_d * 2 ** 0.5 + min_dlzka
    juhovychod = jv0_d * 2 ** 0.5 + min_dlzka
    juhozapad = jz0_d * 2 ** 0.5 + min_dlzka
    vysledok = [sever, severovychod, vychod, juhovychod, juh, juhozapad, zapad, severozapad]
    return vysledok


print(strany_osemuholnika(400, 300))

Táto úloha je zameraná na:

• použitie stratégie riešenia problémov - nakreslenie obrázku, dekompozícia problému na podproblémy a hľadanie vzorov,

• precvičenie príkazov volania funkcie s parametrami a návratovou hodnotou, generovania náhodných čísel a použitie aritmetických operácií.

Vaše zaujímavé riešenia a najčastejšie chyby

Do riešenia úlohy sa zapojilo 20 tímov z kategórie GURU. Plný počet bodov bohužiaľ nezískal žiaden tím. Len 6 tímov použilo v svojich riešeniach generátory desatinných náhodných čísel. Zaijímavé rekurzívne riešenie odovzdal tím timon a ema.

V riešeniach sme zaregistrovali nasledovné nedostatky, vychádzajúce najčastejšie z nedôslednej analýzy problému:

• ignorovanie podmienky, že osemuholník leži na hranici obdĺžnikovej parcely nie mimo nej,

• zjednodušenie riešenia úlohy použitím generátora celočíselných náhodných čísel, ktorým sa generovali len celočíselné dĺžky 4 strán alebo sa generovali desatinné náhodné čísla s nejakým obmedzením rozsahu (npar. len do polovice dĺžky strany),

• neošetrenie podmienky riešiteľnosti, dôsledkom čoho bolo generovanie záporných hodnôt dĺžok osemuholníka,

• nepresnosti vo výpočte spôsobené použitím funkcie na zaokrúhľovanie čísel,

• riešenie úlohy len pre vstupy, kde prvý parameter bol väčší ako druhý parameter,

• vrátenie výsledku s rovnakými dĺžkami dvojíc strán (generovanie len symetrických osemuholníkov),

• namiesto vrátenia osmice čísel vykreslenie obrázku osmeuholníka,

• namiesto vrátenia hodnoty jej vypísanie v tele funkcie.