PALMA junior
Úloha o výťahu v ZOO

Autorské riešenie
[stiahni py, py]

• Počet riešiteľov: 25 / 35 =  71.00 %

• Úspešnosť riešenia: 3,52 / 7 = 50.29 %

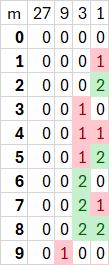
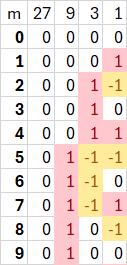
Podľa zadania úlohy máme pre zadanú hmotnosť zvieraťa určiť spôsob ako umiestniť závažia s kilogramážou {1, 3, 9, 27, ...} do oboch košíkov na vyváženie zvieraťa.

Keďže máme vyjadriť celočíselnú hmotnosť zvieraťa ako súčet mocnín trojky ponúka sa použitie trojkového zápisu čísla reprezentujúceho zadanú hmotnosť. Pozrime sa na zápis prvých 10 nezáporných celých čísel v trojkovej sústave:

0₁₀ = 0 × 9 + 0 × 3 + 0 × 1 = 0₃

1₁₀ = 0 × 9 + 0 × 3 + 1 × 1 = 1₃

2₁₀ = 0 × 9 + 0 × 3 + 2 × 1 = 2₃

3₁₀ = 0 × 9 + 1 × 3 + 0 × 1 = 10₃

4₁₀ = 0 × 9 + 1 × 3 + 1 × 1 = 11₃

5₁₀ = 0 × 9 + 1 × 3 + 2 × 1 = 12₃

6₁₀ = 0 × 9 + 2 × 3 + 0 × 1 = 20₃

7₁₀ = 0 × 9 + 2 × 3 + 1 × 1 = 21₃

8₁₀ = 0 × 9 + 2 × 3 + 2 × 1 = 22₃

9₁₀ = 1 × 9 + 0 × 3 + 0 × 1 = 100₃

V zápise niektorých trojkových čísel sa vyskytuje číslica 2, ktorá znamená dvojnásobok hodnoty pri danom rade. V kontexte zadania úlohy to znamená, že niektoré závažia sa použijú dvakrát. To je však neprípustné, lebo v zadaní úlohy sú v sade závaží hmotnosti uvedené len raz. Na druhej strane  je v zadaní uvedené, že závažia sa môžu klásť do oboch košíkov.  Ak si uvedemíme rovnosť 2₃ = 10₃  - 1₃, tak dvojky v zápise čísla môžeme nahradiť tak, že na druhého košíka so závažiami umiestníme závažie s nasledujúcou mocninou trojky (10₃) a do prvého košíka so zvieraťom umiestníme závažie s danou mocnonou trojky (-1₃), Na nasledovnom obrázku sú zobrazené dve tabuľky: so zápisom čísla v trojkovej sústave  (obrázok vľavo) a so zápisom čísla vo vybalansovanej  trojkovej sústave, ktorá používa číslice z množiny {-1, 0, 1} (obrázok vpravo).

Riešenie úlohy môže pozostávať z dvoch krokov. V prvom kroku prevedieme číslo (predstavujúce hmotnosť zvieraťa) do trojkovej sústavy. A v druhom kroku nahradíme všetky dvojky v zápise čísla jednotkami a mínus jednotkami. Pričom hodnoty s mocninami trojky budeme pridávať buď do košíka so zvieraťom (mínus jednotky) alebo do kočíka so závažiami (plus jednotky).

Výsledný program môže vyzerať napr. nasledovne:

def prevod_do_trojkovej_sustavy(cislo):  
    if cislo == 0:
        return [0]
    cifry = []
    while cislo > 0:
        cifry.append(cislo % 3)
        cislo = cislo // 3
    return cifry


def vyvazenie(hmotnost):
    cifry = prevod_do_trojkovej_sustavy(hmotnost)
    prenos = 0
    for i in range(len(cifry)):
        if prenos == 1:
            cifry[i] = cifry[i] + 1
        if cifry[i] == 3:
            cifry[i] = 0
            prenos = 1
        elif cifry[i] == 2:
            cifry[i] = -1
            prenos = 1
        else:
            prenos = 0
    if prenos == 1:
        cifry.append(1)
    kosik_1 = [3 ** x for x in range(len(cifry)) if cifry[x] == -1]
    kosik_2 = [3 ** x for x in range(len(cifry)) if cifry[x] == 1]
    return kosik_1, kosik_2


print(vyvazenie(23))

Iné kratšie riešenie dosiahneme, ak budeme postupne prevádzať číslo predstavujúce hmotnosť zvieraťa do trojkovej sústavy a zároveň rozdeľovať mocniny trojky do košíka so zvieraťom (pri zvyšku 2 po delení trojkou) alebo do košíka so závažiami (pri zvyšku 1 po delení trojkou).

Výsledný program môže vyzerať napríklad nasledovne:

def vyvazenie(hmotnost):
    exponent = 0
    kosiky = ([], [])
    while hmotnost > 0:
        zvysok = hmotnost % 3
        if zvysok == 1:
            kosiky[1].append(3 ** exponent)
        elif zvysok == 2:
            kosiky[0].append(3 ** exponent)
            hmotnost += 1
        hmotnost = hmotnost // 3
        exponent += 1
    return kosiky


print(vyvazenie(23))

Táto úloha je zameraná na:

• použitie stratégie riešenia problémov - dekompozícia problému na podproblémy a hľadanie vzorov,

• precvičenie príkazov volania funkcií s parametrami a návratovou hodnotou, cyklu while, metód zoznamov, celočíslené delenie a zvyšok po delení.

Vaše zaujímavé riešenia a najčastejšie chyby

Do riešenia úlohy sa zapojilo 25 tímov z kategórie GURU. Plný počet bodov za svoje riešenie získali tímy didzej jano, file-open, sigma, t2%sc2cltpm a ubuntulovers, ktorým srdečne gratulujeme. Obzvlášť oceňujeme stručné riešenie tímu sigma (uvedené vyššie) a tiež rekurzívne riešenie tímu didzej jano.

V riešeniach sme zaregistrovali nasledovné nedostatky, vychádzajúce najčastejšie z nedôslednej analýzy problému:

• nesprávne pochopenie zadania úlohy, keď niektorí súťažiaci namiesto jednej sady závaží 1, 3, 9, 27, ... použili

  •  sadu závaží 1,1, 2, 5, 10, 10, 20 ... rozšírenú o sadu závaží 1, 3, 9, 27, ...

  • alebo viaceré sady závaží 1, 3, 9, 27, ...

• vyriešenie úlohy len pre niektoré vstupné hodnoty hmotností zvierat,

• použitie len obmedzeného počtu zavaží (6),

• prása s desatinnými namiesto celými číslami,

• nepresnosti vo výpočte pri niektorých vstupoch spôsobené použitím funkcie round (), kde sa správne mala použiť funkcie floor(),

• namiesto vrátenia hodnoty jej vypísanie v tele funkcie.