PALMA junior
Úloha o transformácii údajov

Autorské riešenie
[stiahni py]                                       

• Počet riešiteľov: 34 / 34 = 100  %                       

• Úspešnosť riešenia:  6.41 / 7 = 92 %                   

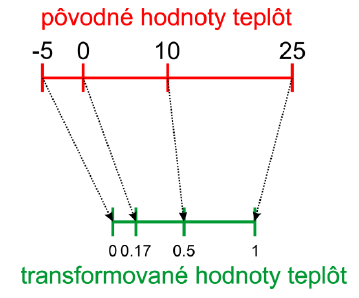
Vstupom pre túto úlohu bol zoznam hodnôt, ktorý bolo potrebné transformovať na zoznam s novým rozsahom hodnôt, ktorý by však zachovával pomer vzdialeností medzi pôvodnými hodnotami, napríklad podľa nasledujúceho obrázka:

Potrebujeme teda vypočítať rozdiel medzi minimálnou a maximálnou hodnotou pôvodného intervalu (dĺžka pôvodného intervalu), v príklade na obrázku max_hodnota-min_hodnota = 25-(-5)=30. Následne určíme relatívnu polohu vybranej hodnoty starého zoznamu v rámci pôvodného intervalu, napríklad na obrázku relativna_poloha=(hodnota - min_hodnota)/(max_hodnota-min_hodnota) = 10-(-5)/30=0,5. Dostali sme teda, že hodnota 10 leží v strede pôvodného intervalu. Následne vypočítame normalizovanú hodnotu v novom zozname s využitím tejto relatívnej polohy:

normalizovana_hodnota = dolna_hranica + relativna_poloha * (horna_hranica - dolna_hranica) =

= 0 + 0,5*(1-0)= 0,5.

Tento postup zopakujeme pre všetky hodnoty pôvodného zoznamu.

Nasleduje možný zdrojový kód v jazyku Python:

def transformuj_zoznam(zoznam, dolna_hranica, horna_hranica):
    min_hodnota = min(zoznam)
    max_hodnota = max(zoznam)
    normalizovany_zoznam = []
    for cislo in zoznam:
        relativna_poloha = (cislo - min_hodnota) / (max_hodnota - min_hodnota)
        normalizovana_hodnota = dolna_hranica + relativna_poloha * (horna_hranica - dolna_hranica)
        normalizovany_zoznam.append(normalizovana_hodnota)
    return normalizovany_zoznam

Vaše zaujímavé riešenia a najčastejšie chyby

Úlohu riešilo 34 tímov. Väčšina tímov použila správny postup na dosiahnutie vhodného riešenia a využilo postup uvedený v autorskom riešení. Viaceré riešenia boli výborne okomentované. V niektorých riešeniach tímy správne určili minimálnu a maximálnu hodnotu zoznamu a vypočítali normalizované hodnoty pre minimálny a maximálny stupeň. Nesprávne však bola vypočítaná normalizovaná hodnota, ktorú bolo potrebné určiť pomocou vzťahu (hodnota-min)/(max-min).