Autorské riešenie
Skákanie po bielych pásoch na priechode pre chodcov alebo stúpanie len na čiary medzi dlaždicami sú zábavné činnosti, ktoré už vyskúšal asi každý z nás. Ak však máme takýto pohyb vopred naplánovať, navyše tak, aby bol najúspornejší, už to nevyzerá tak zábavne. Pozrime sa na to, čo plánovanie takéhoto pohybu po mriežkovom chodníku zahŕňa:
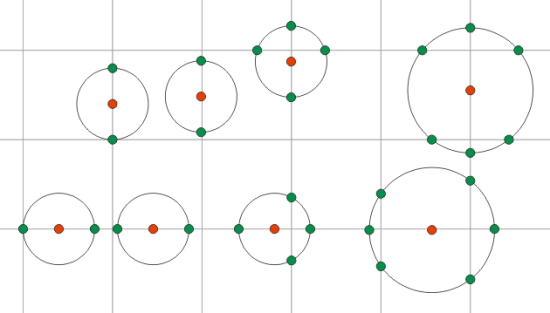
Vďaka tomuto postupu sme veľký problém rozdelili na niekoľko menších. Poďme ich postupne riešiť. Body mriežky, na ktoré je možné z aktuálneho bodu vstúpiť Na obrázku nižšie je niekoľko prípadov, kde môže smerovať krok z aktuálneho bodu:
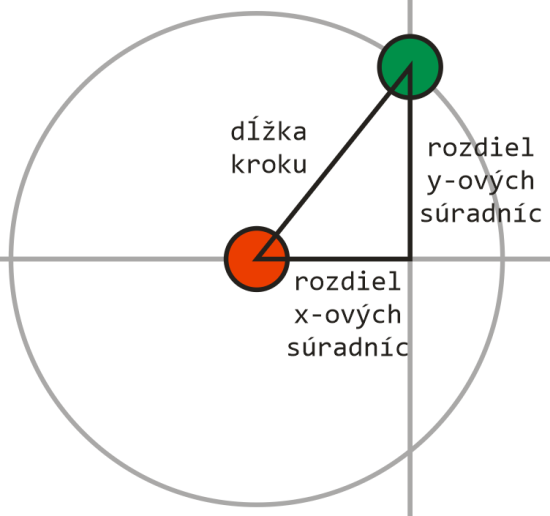
Aj keď to vyzerá komplikovane, vieme to vyriešiť. Poznáme súradnice aktuálneho, červeného bodu. Jednu zo súradníc každého zeleného bodu vieme tiež. Buď je taká istá ako celočíselná súradnica červeného bodu, alebo je najbližšia celočíselná k neceločíselnej súradnici červeného bodu. Inak povedané, máme dva body v rovine a ich vzdialenosť. Jediné či nepoznáme je jedna zložka jednej zo súradníc jedného bodu. Túto vieme nájsť pomocou Pytagorovej vety:
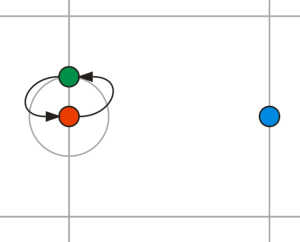
Riešenie tejto časti môže vyzerať nasledovne: def ries_kvad_rovnicu(a, b, c): d = b ** 2 - 4 * a * c if d < 0: return [] if d == 0: return [-b / (2 * a)] return [(-b + d ** 0.5) / (2 * a), (-b - d ** 0.5) / (2 * a)] def vypocitaj_suradnicu(x, y, nove_x, nove_y, dlzka_kroku): if nove_x is None: a = 1 b = -2 * x c = x ** 2 + (y - nove_y) ** 2 - dlzka_kroku ** 2 x_suradnice = ries_kvad_rovnicu(a, b, c) return [[nove_x, nove_y] for nove_x in x_suradnice] if nove_y is None: a = 1 b = -2 * y c = y ** 2 + (x - nove_x) ** 2 - dlzka_kroku ** 2 y_suradnice = ries_kvad_rovnicu(a, b, c) return [[nove_x, nove_y] for nove_y in y_suradnice] def suradnice_po_kroku(aktualna_suradnica, dlzka_kroku): x = aktualna_suradnica[0] y = aktualna_suradnica[1] suradnice = [] if x == int(x): # x-ova je cele cislo suradnice.extend(vypocitaj_suradnicu(x, y, None, math.floor(y), dlzka_kroku)) suradnice.extend(vypocitaj_suradnicu(x, y, x, None, dlzka_kroku)) suradnice.extend(vypocitaj_suradnicu(x, y, None, math.floor(y) + 1, dlzka_kroku)) if y == int(y): # y-ova je cele cislo suradnice.extend(vypocitaj_suradnicu(x, y, math.floor(x), None, dlzka_kroku)) suradnice.extend(vypocitaj_suradnicu(x, y, None, y, dlzka_kroku)) suradnice.extend(vypocitaj_suradnicu(x, y, math.floor(x) + 1, None, dlzka_kroku)) suradnice_bez_duplicit = [] for suradnica in suradnice: if suradnica not in suradnice_bez_duplicit: suradnice_bez_duplicit.append(suradnica) return suradnice_bez_duplicit Funkcia suradnice_po_kroku zistí a vráti zoznam súradníc, kam je možné sa dostať z aktuálnej súradnice pri zadanej dĺžke kroku. Keďže niektoré zo súradníc by mohli byť duplicitné, z výsledného zoznamu ich odstránime. Funkcia vypocitaj_suradnicu vypočíta a vráti súradnice nových bodov, kde jedna zložka z ich súradníc je neznáma. Ak vyžijeme Pytagorovu vetu, dostaneme sa ku kvadratickej rovnici. Na jej riešenie sme si vytvorili funkciu ries_kvad_rovnicu. Bod, ktorý nás najviac priblíži k cieľu 1 Jedna z možností ako vybrať ten "správny" bod, je jeho priama vzdialenosť od cieľa. Ak použijeme túto metriku, riešenie môže vyzerať nasledovne: def vzdialenost1(bod1, bod2): return ((bod1[0] - bod2[0]) ** 2 + (bod1[1] - bod2[1]) ** 2) ** 0.5 def vrat_suradnice_pohybu1(start, ciel, dlzka_kroku): aktualna_suradnica = start suradnice_pohybu = [start] while vzdialenost1(aktualna_suradnica, ciel) > dlzka_kroku: potencialne_suradnice = suradnice_po_kroku(aktualna_suradnica, dlzka_kroku) najlepsia_suradnica = None najblizsie_k_cielu = float('inf') for potencialna_suradnica in potencialne_suradnice: if potencialna_suradnica not in suradnice_pohybu: if vzdialenost1(potencialna_suradnica, ciel) < najblizsie_k_cielu: najlepsia_suradnica = potencialna_suradnica najblizsie_k_cielu = vzdialenost1(potencialna_suradnica, ciel) suradnice_pohybu.append(najlepsia_suradnica) aktualna_suradnica = najlepsia_suradnica suradnice_pohybu.append(ciel) return suradnice_pohybu Všimnime si, že ako kritérium používame priamu vzdialenosť, ale body pohybu vyberáme tak, aby boli umiestnené na mriežke. Takto by s nám mohlo stať, že by sme uviazli v nekonečnej slučke medzi dvoma bodmi:
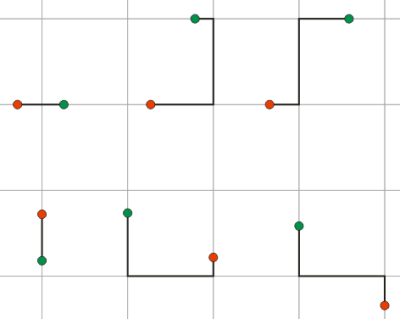
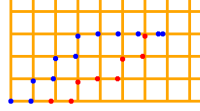
Ak začneme v červenom bode, najviac nás k cieľu (modrý bod) priblíži zelený bod. Ak sa presunieme do zeleného bodu, najviac nás k cieľu priblíži červený bod. Aby sme v takejto slučke neuviazli, uvažujeme len tie body, v ktorých sme ešte neboli. Bod, ktorý nás najviac priblíži k cieľu 2 Pre výber toho správneho bodu môžeme využiť aj inú metriku. Pozrime sa, ako nás nový bod priblíži k cieľu, ak by sme išli po čiarach mriežky. Výpočet mriežkovej vzdialenosti bude o niečo náročnejší, pretože musíme uvažovať rôzne prípady:
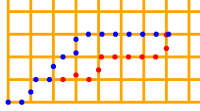
V tomto prípade by riešenie mohlo vyzerať takto: def vzdialenost2(bod1, bod2): x1, y1 = bod1 x2, y2 = bod2 if y1 == y2: dx = abs(x1 - x2) elif math.floor(x1) == math.floor(x2): dx = min(x1 % 1 + x2 % 1, 2 - (x1 % 1 + x2 % 1)) else: dx = abs(x1 - x2) if x1 == x2: dy = abs(y1 - y2) elif math.floor(y1) == math.floor(y2): dy = min(y1 % 1 + y2 % 1, 2 - (y1 % 1 + y2 % 1)) else: dy = abs(y1 - y2) return dx + dy def vrat_suradnice_pohybu2(start, ciel, dlzka_kroku): aktualna_suradnica = start suradnice_pohybu = [start] while vzdialenost1(aktualna_suradnica, ciel) > dlzka_kroku: potencialne_suradnice = suradnice_po_kroku(aktualna_suradnica, dlzka_kroku) najlepsia_suradnica = None najblizsie_k_cielu = vzdialenost2(aktualna_suradnica, ciel) najblizsie_k_cielu = float('inf') for potencialna_suradnica in potencialne_suradnice: if vzdialenost2(potencialna_suradnica, ciel) < najblizsie_k_cielu: najlepsia_suradnica = potencialna_suradnica najblizsie_k_cielu = vzdialenost2(potencialna_suradnica, ciel) suradnice_pohybu.append(najlepsia_suradnica) aktualna_suradnica = najlepsia_suradnica suradnice_pohybu.append(ciel) return suradnice_pohybu Otázka je, ktorý z týchto prístupov je lepší? Odpoveď nie je jednoduchá a v podstate neexistuje. V rôznych situáciách môžu byť tieto prístupy rôzne úspešné. Pozrime sa napríklad na nasledujúce dve situácie. Červenou farbou je riešenie prvým prístupom, modrou farbou riešenie druhým prístupom.
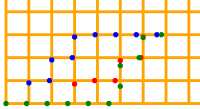
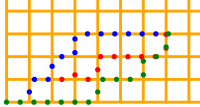
Natíska sa otázka, či existuje spôsob, ktorý by našiel prechod na najmenší možný počet krokov bez ohľadu na situáciu. Ukážme si jeden z nich. V situáciách, kde potrebujeme nájsť najlepšie riešenie a nemáme dostatok vedomostí na to, aby sme ho priamo našli, môžeme využiť iný prístup. Nájdime všetky prípustné riešenia a vyberme z nich to najlepšie. Prípustné v tomto prípade znamená, že neuvažujeme riešenia, kde by sme sa od cieľa vzďaľovali (podľa akej metriky?), kde by sme opakovane navštevovali rovnaké body a pod. Z každého aktuálne bodu teda nevykročíme len jedným smerom, ale postupne vykročíme všetkými relevantnými smermi. Keď sa nám podarí dostať do cieľa tak skontrolujeme, či táto práve zavŕšená cesta nie je tou najlepšou doposiaľ nájdenou. Ak áno, zapamätáme si ju. Riešenie týmto prístupom môže vyzerať napr. takto: def najdi_najlepsiu_cestu(start, ciel, dlzka_kroku, suradnice_pohybu=[], naj_suradnice_pohybu=[]): suradnice_pohybu.append(start) if start == ciel: if naj_suradnice_pohybu == [] or \ len(suradnice_pohybu) < len(naj_suradnice_pohybu): naj_suradnice_pohybu.clear() naj_suradnice_pohybu.extend(suradnice_pohybu) elif vzdialenost1(start, ciel) <= dlzka_kroku: najdi_najlepsiu_cestu(ciel, ciel, dlzka_kroku, suradnice_pohybu, naj_suradnice_pohybu) else: suradnice_kroku = suradnice_po_kroku(start, dlzka_kroku) for suradnica in suradnice_kroku: if vzdialenost2(suradnica, ciel) < vzdialenost2(start, ciel): najdi_najlepsiu_cestu(suradnica, ciel, dlzka_kroku, suradnice_pohybu, naj_suradnice_pohybu) suradnice_pohybu.pop() def vrat_suradnice_pohybu3(start, ciel, dlzka_kroku): suradnice_pohybu = [] naj_suradnice_pohybu = [] najdi_najlepsiu_cestu(start, ciel, dlzka_kroku, suradnice_pohybu, naj_suradnice_pohybu) return naj_suradnice_pohybu Funkcia vrat_suradnice_pohybu3 ku svojim trom parametrom vytvorí ešte dve premenné. V zozname suradnice_pohybu si budeme zaznamenávať súradnice cesty, ktorú práve skúmame a v zozname naj_suradnice_pohybu si budeme uchovávať najlepšiu z ciest, ktoré sme doposiaľ preskúmali. Funkcia najdi_najlepsiu_cestu sa postará o systematické prehľadanie všetkých ciest. Všimnime si ešte, ako sme vyriešili požiadavku na prípustné riešenia. Z možných krokov preskúmame len tie, ktoré znížia mriežkovú vzdialenosť k cieľu. Vieme totiž, že ak by sme uvažovali priamu vzdialenosť, niekedy by krok, ktorý by nás priblížil k cieľu, nebol možný. Porovnajme výsledky, ktoré nájde takéto riešenie (zelená farba):
Aj keď posledný prístup nájde najlepšie riešenie, netešme sa predčasne. Preskúmať všetky cesty je pomerne náročné. Ak by sme z každého bodu uvažovali len dve možnosti (v skutočnosti ich môže byť aj viac) ako vykročiť, pri dĺžke cesty 10 krokov by to bolo 1024 možných ciest. Pri dĺžke cesty 20 krokov je to už 1048576 možností. Inak povedané, pri väčších vzdialenostiach by sme sa výsledku nemuseli prakticky ani dočkať. Prakticky je tak lepšie rýchlo dostupné, aj keď nie najlepšie riešenie, než najlepšie riešenie, ktoré je časovo nedostupné. Aby sme nekončili takto pesimisticky. Existujú prístupy, ktoré nájdu najlepšie riešenie a navyše v dostupnom čase. Záujemcom odporúčame pozrieť sa napr. na dynamické programovanie. Vaše zaujímavé riešenia a najčastejšie chyby Toto je optimalizačná úloha, v ktorej bolo potrebné najskôr identifikovať možné kroky a potom optimalizovať, ktoré z nich použiť. S týmto si poradila, alebo takmer poradila polovica z vás. Niektorí z vás uvažovali len konkrétny smer pohybu alebo konkrétnu súradnicu štartu. |
||||||||||||||||||
|
© Univerzita Pavla Jozefa Šafárika v Košiciach, Prírodovedecká fakulta, Ústav informatiky palmaj (zavinac) upjs.sk |
||||||||||||||||||