Autorské riešenie
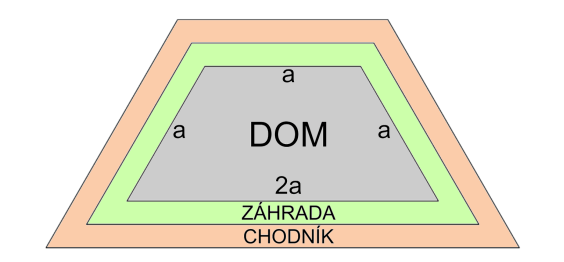
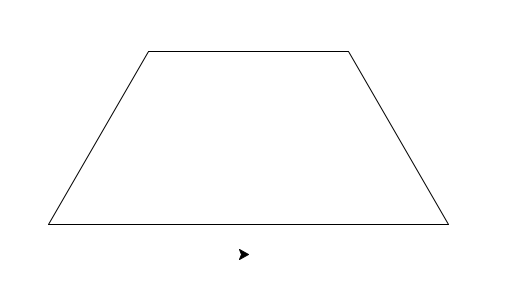
V Korytnačkove sa buduje nová moderná štvrť pre mladé rodiny. Vízia starostu Korytnačkova je, aby všetky domy v štvrti vyzerali nadčasovo. Domy musia mať tvar lichobežníka s určenými dĺžkami strán (pozri obrázok nižšie).
Z obrázku zo zadania je zrejmé, že daný nárys domu so záhradou a chodníkom je reprezentovaný troma lichobežníkmi. Z obrázku ale aj zo zadania čítame, že záhradu a chodník reprezentujú pásy medzi danými lichobežníkmi. Taktiež je spomenuté že pásy sú rovnakej šírky (Pásy predstavujúce záhradu a chodník sú rovnako široké). Je zrejmé, že veľkosť záhrady a chodníka bude závisieť práve od šírky daných pásov. Našou úlohou je teda naprogramovať funkciu kresli() s dvomi parametrami ? veľkosti strany domu a šírkou pásu.
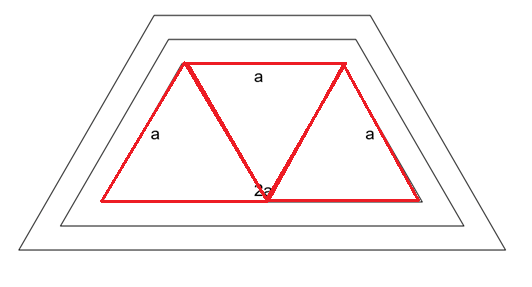
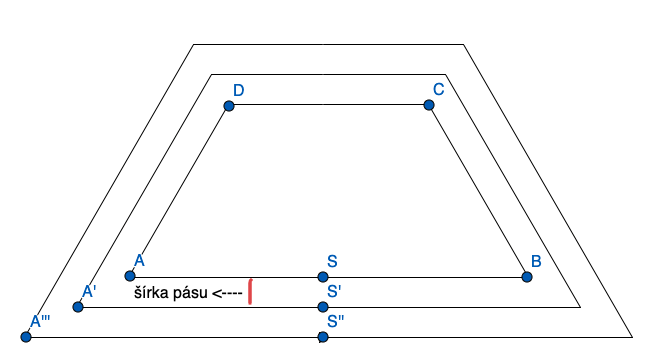
Teraz už vidíme, že uhly pri základniach sú 60 stupňov. Nie je problém si dorátať ani zvyšné uhly. Ak poznáme vnútorné uhly a dĺžky strany, môžeme vykresľovať lichobežník. Keďže pre riešenie úlohy je potrebné vykresliť až tri lichobežníky, je rozumné si na ich vykreslenie vytvoriť funkciu ktorú opakovane použijeme. Pre funkciu vykreslenia lichobežníka by stačil aj jeden parameter dlzka_strany. V tom prípade by ale funkciu s týmto jedným parametrom nebolo možné použiť viackrát, keďže pre lichobežníky predstavujúce záhradu a chodník už neplatí, že strany sú v pomere 2a : a : a : a. Ako uvidíme nižšie, dolná základňa týchto lichobežníkov sa bude zväčšovať o inú hodnotu ako horná základňa a ramená, čo nezachová spomínaný pomer. Preto pre opakované použitie funkcie, je vodné použiť tri parametre reprezentujúce strany všeobecného rovnoramenného lichobežníka (dolna_zakladna, rameno, horna_zakladna). Ešte pred samotnou funkciou sa zamyslíme odkiaľ je vhodné začať lichobežník vykresľovať. Vieme že po vykreslení prvého lichobežníka sa musíme posunúť na vhodnú pozíciu pre vykreslenie ďalšieho. Ako sme uviedli parameter reprezentujúci šírku pásu určuje o akú vzdialenosť je potrebné sa posunúť. Aj z matematiky sme zvyknutí načrtávať lichobežník z od dolnej základne z ľavého vodu (na obrázku nižšie bod A). Ak by sme sa ale chceli presunúť o úroveň nižšie do bodu A?, museli by sme si následný posun prerátavať a nevedeli by sme hodnotu z parametra použiť priamo. Preto je vhodnejšie začať vykresľovať lichobežníky zo stredu dolnej základne (na obrázku nižšie bod S). Ak sa v tomto prípade chceme posunúť na ďalšiu úroveň (na obrázku nižšie bod S?), stačí sa iba otočiť a posunúť o hodnotu v parametri funkcie, reprezentujúcu práve tento posun. Zároveň to že poznáme dĺžku dolnej základne, vieme o koľko je potrebné sa posunúť pri vykresľovaní lichobežníka.
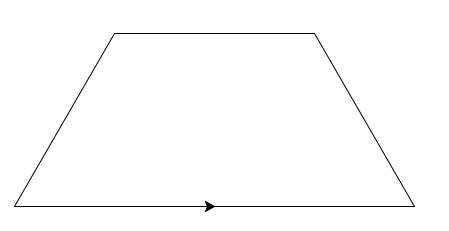
Ak už vieme, že vykresľovanie začne od stredu dolnej základne, funkcia lichobežník môže vyzerať nasledovne: #Python def lichobeznik(polovica_dolna_zakladna, rameno, horna_zakladna): pero.forward(polovica_dolna_zakladna) pero.left(120) pero.forward(rameno) pero.left(60) pero.forward(horna_zakladna) pero.left(60) pero.forward(rameno) pero.left(120) pero.forward(polovica_dolna_zakladna) Po vykreslení lichobežníka je potrebné sa posunúť na ďalšiu úroveň pre vykreslenie ďalšieho. Keďže vykresľujeme lichobežníky z vnútra (nakoľko rozmery domu sú reprezentované parametrami funkcie kresli()), posúvame sa k strednému lichobežníku. Keďže sa budeme posúvať ešte raz kvôli tretiemu lichobežníku, je vhodné si na samotný posun vytvoriť osobitnú funkciu. Ako sme spomínali, posun reprezentuje šírku pásov medzi lichobežníkmi. Táto vzdialenosťou je zároveň parametrom aj funkcie kresli(). Bude preto aj parametrom funkcie pre posun. Po vykreslení je korytnačka v počiatočnej pozícií (ako na obrázku nižšie).
Ako sme spomínali chceme sa posunúť opäť na stred druhého lichobežníka. Stredy dolných základní všetkých troch lichobežníkov sú na jednej osi. Pre posunutie na novú pozíciu sa stačí otočiť doprava, posunúť o zadaná vzdialenosť a otočiť sa späť. Netreba zabúdať na zdvihnutie a položenie pera. Funkcia posun() môže vyzerať nasledovne: #Python def posun(vzdialenost): pero.right(90) pero.penup() pero.forward(posun) pero.left(90) pero.pendown() Po posune je korytnačka v tejto pozícií. A je pripravená na vykreslenie ďalšieho lichobežníka.
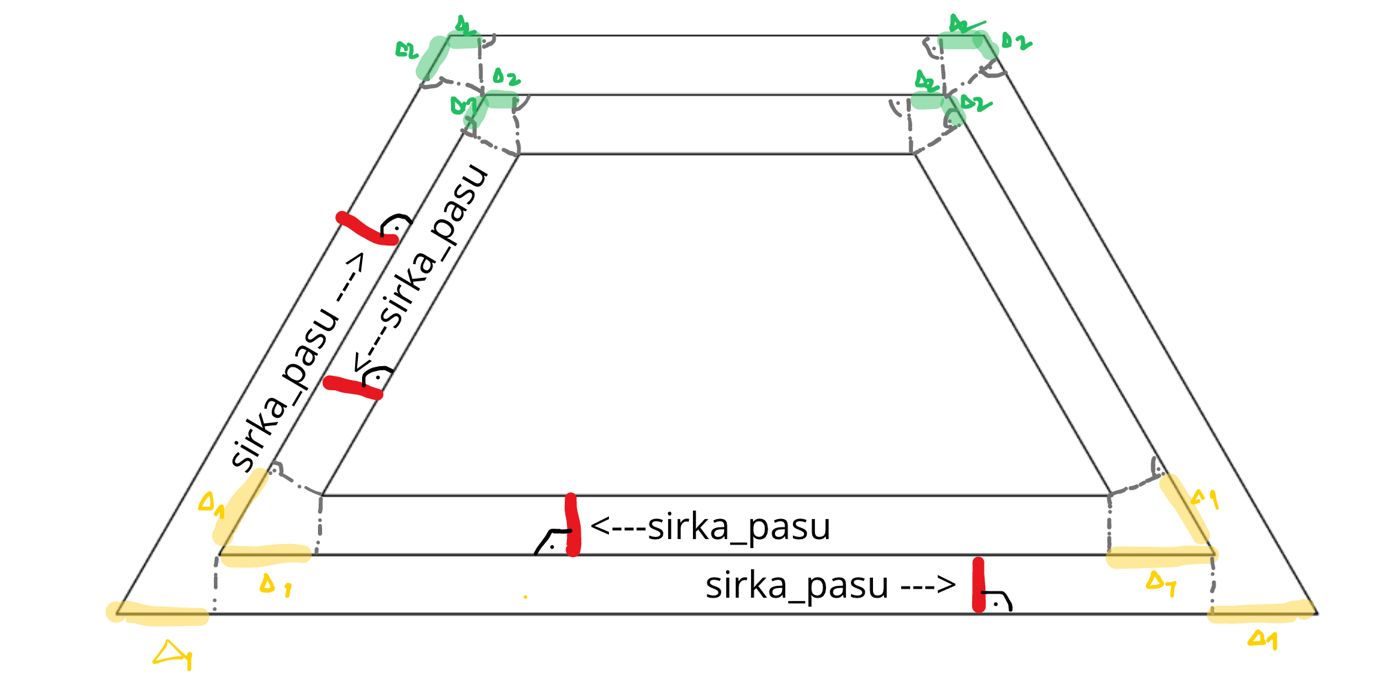
Teraz pokračujeme vykreslením druhého lichobežníka. Správnym náčrtom jednoducho zistíme že veľkosť novej dolnej základne je veľkosť pôvodnej + 2*vhodný prírastok (na obrázku označený ako Δ1 (delta1)). Podobne pre hornú základňu ide o prírastok Δ2 (delta2) ktorý taktiež pripočítame dvakrát ku veľkosti pôvodnej hornej podstavy. Už ľahko vidno (na obrázku nižšie) že pre veľkosť ramená druhého lichobežníka platí, že je to veľkosť pôvodného+ Δ1 +Δ2.
Z obrázku si taktiež môžeme všimnúť že aj pre tretí (vonkajší) lichobežník platí že jeho
A ako tie prírastky (delty) správne vypočítať? Aj to je jeden z dôvodov prečo je dôležité urobiť si dobrý náčrt ! Z obrázku si vieme všimnúť pri vrcholoch dva pravouhlé trojuholníky. Na obrázku nižšie sú zobrazené dva z nich na výpočet delta1 a detla2.
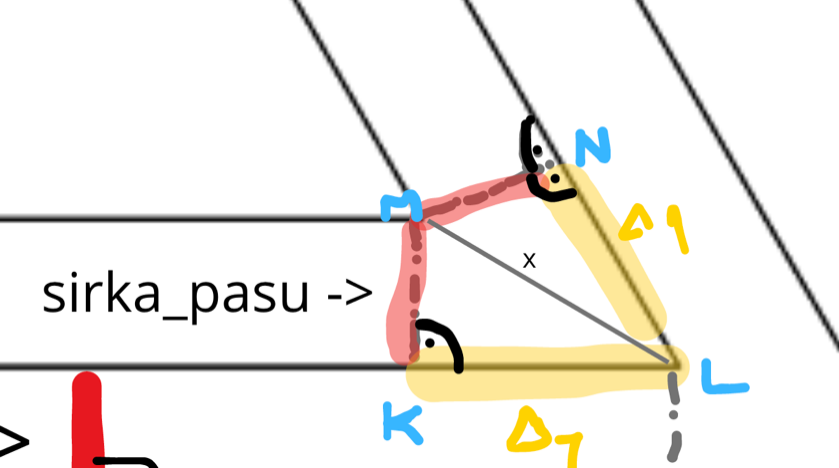
Pre nás je dôležitý výpočet práve Δ1. K tomu je ale nutné poznať stranu v obrázku označenú ako x. Nakoľko trojuholník MKL je polovica rovnoramenného trojuholníka MM′L so stranou 2 * sirka_pasu, je strana x rovná práve 2 * sirka_pasu. Preto pre výpočet Δ1 (delta1) môžeme využiť Pytagorovu vetu nasledovne: (sirka_pasu)2 + (Δ1)2 = (2 * sirka_pasu)2 (Δ1)2 = 4 * (sirka_pasu)2 - (sirka_pasu)2 (Δ1)2 = 3 * (sirka_pasu)2 Δ1 = √3 * sirka_pasu (uvažujeme len kladné hodnoty) #Python delta1 = math.sqrt((2 * sirka_pasu) ** 2 - (sirka_pasu ** 2)) Keďže trojuholník MNL je s MKL zhodný, výpočet bude rovnaký a preto aj delta1 bude na ramene rovnaká.
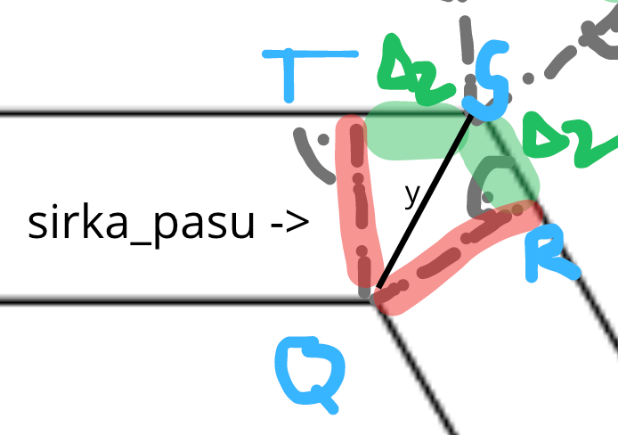
Pre výpočte delta2 je myšlienka rovnaká. Zmena je v hodnote y (z obrázka vyššie) a taktiež pravouhlé trojuholníky budú s inými stranami. Trojuholník STQ je pravouhlý s pravým uhlom pri vrchole T. Znova ide polovicu rovnoramenného trojuholníka no tentokrát so stranou 2* Δ2. Preto aj strana y (z obrázka) má veľkosť 2 * Δ2. Na výpočet Δ2 preto môžeme využiť taktiež Pytagorovu vetu nasledovne: (sirka_pasu)2 + (Δ2)2 =(2 * Δ2)2 (sirka_pasu)2 = 4 * (Δ2)2 - (Δ2) (sirka_pasu)2 / 3 = (Δ2)2 Δ2 = sirka_pasu / √3 Taktiež s trojuholníkom STX je trojuholník SRQ zhodný preto prírastok delta2 na ramene bude rovnaký. #Python delta2 = sirka_pasu / math.sqrt(3) Ešte je dôležité si uvedomiť čo nám dovoľuje počítať s pravouhlým trojuholníkom. To že ide ozaj o polovicu rovnoramenného trojuholníka (čo nám dovoľuje výpočet so zadanými stranami pomocou Pytagorovej vety) vychádza z uhlov ktoré si vieme dopočítať v daných trojuholníkoch. Na uvedomenie tejto skutočnosti, pomôže obrázok nižšie.
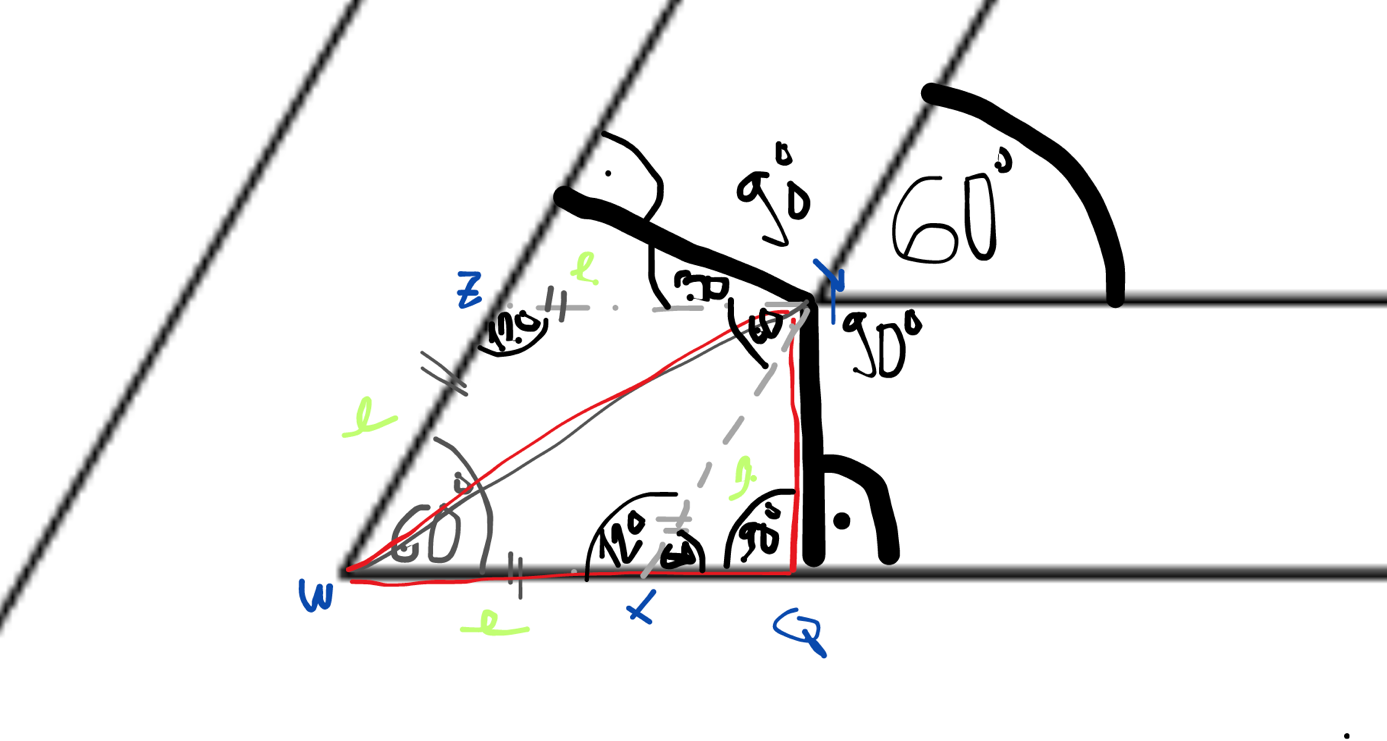
Keďže trojuholník WXY (taktiež WZY) je rovnoramenný so stranami l tak v trojuholníku WXY musia byť aj uhly pri vrcholoch W a Y rovnaké. Do 180 stupňov v danom trojuholníku ostáva 60 stupňov, ktoré po rovnakom rozdelení pre 2 vrcholy dostávame 30 stupňov. Už ľahko vidíme aké budú uhly WQY. Pri vrchole Q je prvý uhol a teda 90 stupňov. Pri vrchole W z predchádzajúceho výpočtu 30 stupňov. Z toho pri vrchole Y trojuholníka WQY bude 60 stupňov. Teraz už vidíme že ozaj ide o polovicu rovnoramenného trojuholníka a naše výpočty pre delta1 a delta2 boli správne.
Vieme využiť funkcie ktoré sme si pripravili a využiť vo funkcii kresli() s vhodnými parametrami (ktoré využívame). Kód môže vyzerať nasledovne: #Python def kresli(dlzka_strany, sirka_pasu): lichobeznik(dlzka_strany, dlzka_strany, dlzka_strany) posun(sirka_pasu) delta_jedna = math.sqrt((2 * sirka_pasu) ** 2 - (sirka_pasu ** 2)) delta_dva = sirka_pasu / math.sqrt(3) lichobeznik(dlzka_strany + delta_jedna, dlzka_strany + delta_jedna + delta_dva, dlzka_strany + 2 * delta_dva) posun(sirka_pasu) lichobeznik(dlzka_strany + 2 * delta_jedna, dlzka_strany + 2 * delta_jedna + 2 * delta_dva, dlzka_strany + 4 * delta_dva) Výsledné riešenie tejto úlohy môže vyzerať nasledovne: #Python import math import turtle def lichobeznik(dolna_zakladna, rameno, horna_zakladna): pero.forward(dolna_zakladna) pero.left(120) pero.forward(rameno) pero.left(60) pero.forward(horna_zakladna) pero.left(60) pero.forward(rameno) pero.left(120) pero.forward(dolna_zakladna) def posun(vzdialenost): pero.right(90) pero.penup() pero.forward(vzdialenost) pero.left(90) pero.pendown() def kresli(dlzka_strany, sirka_pasu): lichobeznik(dlzka_strany, dlzka_strany, dlzka_strany) posun(sirka_pasu) delta1 = math.sqrt((2 * sirka_pasu) ** 2 - (sirka_pasu ** 2)) delta2 = sirka_pasu / math.sqrt(3) lichobeznik(dlzka_strany + delta1, dlzka_strany + delta1 + delta2, dlzka_strany + 2 * delta2) posun(sirka_pasu) lichobeznik(dlzka_strany + 2 * delta1, dlzka_strany + 2 * delta1 + 2 * delta2, dlzka_strany + 4 * delta2) tabula = turtle.Screen() pero = turtle.Turtle() kresli(200, 30) tabula.mainloop() Táto úloha je zameraná na:
Vaše zaujímavé riešenia a najčastejšie chyby Do riešenia úlohy sa zapojilo 32 tímov z kategórie GURU. Plný počet za svoje riešenie dosiahol 1 tím, s názvom file-open, ktorým gratulujeme. Vypracovanú úlohu pomocou korytnačej grafiky odovzdalo 25 tímov. Karteziánsku grafiku použilo 7 tímov. V riešeniach sme zaregistrovali nasledovné nedostatky:
|
||||||||||
|
© Univerzita Pavla Jozefa Šafárika v Košiciach, Prírodovedecká fakulta, Ústav informatiky palmaj (zavinac) upjs.sk |
||||||||||