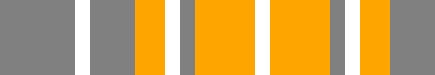PALMA junior
Úloha o fázach Mesiaca

Autorské riešenie
[stiahni py, py]

• Počet riešiteľov: 7 / 9 =  78 %

• Úspešnosť riešenia: 3,13 / 5 = 63 %

Pri vykresľovaní fáz Mesiaca, si treba uvedomiť, či chceme mať zobrazené všetky štyri základné fázy (nov, prvá štvrť, spln, posledná štvrť), alebo len dve základné fázy (nov a spln) ,alebo len jednu základnú fázu (nov).

Najprv si ukážeme riešenie úlohy, v ktorom sú zobrazené aspoň dve základné fázy (nov a spln). V tomto riešení môžeme zadať počet fáz ako ľubovoľné párne číslo. Ak zadaný počet fáz bude deliteľný štyrmi, tak sa zobrazia všetky štyri základné fázy mesiaca.

Pozrime sa lepšie na obrázok so 16 fázami Mesiaca so zadania úlohy.

Ak si vykreslíme pod sebou prvých osem a druhých osem fáz Mesiaca nájdeme veľkú podobnosť medzi obrázkami v oboch riadkoch.

Ak by sme vedeli vykresliť obrázok na prvom riadku so sivou a oranžovou farbou, tak by sme mali vedieť vykresliť aj obrázok na druhom riadku s prehodenými farbami oranžová a sivá. Preto teraz uvažujme ako by sme vykreslili prvých osem fáz. Z obrázku z prvého riadku je zrejmé, že v jednotlivých fázach Mesiaca sa šírka sivého obdĺžnika postupne zmenšuje z 8/8 na 7/8, 6/8, 5/8, 4/8, 3/8, 2/8 až na 1/8 veľkosti štvorca. A šírka oranžového obdĺžnika postupne narastá tak, že v súčte šírky sivého a oranžového obdĺžnika v každej fáze Mesiaca sú rovné veľkosti štvorca,

Vo všeobecnosti vieme určiť šírku sivého obdĺžnika (premenná sirka1) a oranžového obdĺžnika (premenná sirka2) pre každú fázu Mesiaca nasledovne. Ak si označíme premennou pocet_faz zadaný počet fáz Mesiaca, premennou dlzka rozmer štvorca, premennou poradie počítadlo fáz (klesajúce postupne o 1 od hodnoty premennej pocet_faz po 1), tak pre premenné sirka1 a sirka2 platia vzťahy:

sirka1 = poradie / (pocet_faz // 2) * dlzka
sirka2 = dlzka - sirka1

Na vykreslenie obdĺžnika vytvoríme funkciu obdlznik():

def obdlznik(sirka, vyska, farba_pera, farba_pozadia):
    ''' Vykreslí obdĺžnik so zadanými rozmermi a zadanými farbami pera a pozadia '''
    pero.color(farba_pera, farba_pozadia)
    pero.begin_fill()
    for _ in range(2):
        pero.forward(sirka)
        pero.left(90)
        pero.forward(vyska)
        pero.left(90)
    pero.end_fill()

Na vykreslenie dvojfarebnej fázy Mesiaca vytvoríme funkciu vyfarbeny_stvorec():

def vyfarbeny_stvorec(dlzka, poradie, pocet_faz, farba_pera, farba_pozadia1, farba_pozadia2):
    ''' Vykreslí štvorec so zadanou dĺžkou strany a zadanou farbou 
        pera a dvomi farbami pozadia '''
    sirka1 = poradie / (pocet_faz // 2) * dlzka
    sirka2 = dlzka - sirka1
    obdlznik(sirka1, dlzka, farba_pera, farba_pozadia1)
    pero.forward(sirka1)
    obdlznik(sirka2, dlzka, farba_pera, farba_pozadia2)
    pero.forward(sirka2)

Na presunutie sa na obrázok ďalšej fázy vytvoríme funkciu posun():

def posun(dlzka):
    ''' Posunie pero na vykreslenie štvorca s nasledovnou fázou '''
    pero.penup()
    pero.forward(dlzka * 0.2)
    pero.pendown()

Napokon vytvoríme hlavnú funkciu kresli() na vykreslenie zadaného počtu fáz Mesiaca:

def kresli(velkost, pocet_faz):
    ''' Vykreslí zadaný počet fáz mesiaca ako rad štvorcov so zadanou veľkosťou '''
    for i in range(pocet_faz // 2, 0, -1):
        vyfarbeny_stvorec(velkost, i, pocet_faz, 'black', 'gray', 'orange')
        posun(velkost)
    for i in range(pocet_faz // 2, 0, -1):
        vyfarbeny_stvorec(velkost, i, pocet_faz, 'black', 'orange', 'gray')
        posun(velkost)

Kompletné riešenie tejto úlohy je uvedené v súbore fazy_mesiaca.py, na ktorého odkaz je uvedený hore na tejto webovej stránke.

Teraz si ukážeme riešenie úlohy pre ľubovoľný celočíselný počet fáz, v ktorom je zobrazená aspoň fáza nov.

Pozrime sa na náčrt riešenia pre pocet_faz = 5 na obrázku nižšie, kde je zobrazený nov ako prvá fáza Mesiaca, a ostatné základné fázy (spln, dorastanie, cúvanie) nie sú zobrazené.

Pri vykresľovaní týchto piatich fáz budeme postupovať tak, že najprv vykreslíme sivý štvorec a na neho oranžový obdĺžnik s nasledovnými hodnotami počiatočnej a koncovej pozície (vo vodorovnom smere): (5/5, 5/5), (3/5, 5/5), (1/5, 5/5), (0/5, 4/5), (0/5, 2/5).

Podobne pri riešení pre pocet_faz = 6, môžeme sa pozrieť na nasledovný obrázok:

Pri vykresľovaní týchto šiestich fáz budeme postupovať tak, že najprv vykreslíme sivý štvorec a na neho oranžový obdĺžnik s nasledovnými hodnotami počiatočnej a koncovej pozície (vo vodorovnom smere): (6/6, 6/6), (4/6, 6/6), (2/6, 6/6), (0/6, 6/6), (0/6, 4/6), (0/6, 2/6).

Vo všeobecnosti pri vykresľovaní oranžového obdĺžnika sa mení hodnota jeho počiatočnej pozície (vo vodorovnom smere): pocet_faz/pocet faz, pocet_faz-2/pocet faz, pocet_faz-4/pocet fáz, ... kým je výsledok kladný, potom sú ostatné hodnoty rovné 0. A hodnota jeho koncovej pozície (vo vodorovnom smere) je rovná: v prvej polovici zoznamu pocet_faz/pocet faz a v druhej polovici zoznamu pocet_faz/pocet faz, (pocet_faz-2/pocet faz), (pocet_faz-4)/pocet fáz ... 

Výsledný funkciu kresli() môže vyzerať nasledovne:

def kresli(strana, pocet_faz):
    '''Vykreslí zadaný počet fáz mesiaca ako rad štvorcov so zadanou veľkosťou '''
    posun = 2 * strana / pocet_faz

    for pocitadlo in range(pocet_faz):
        pero.pendown()
        obdlznik(strana, strana, 'gray')  # sirka, vyska
        zaciatok_oranzova = max(0, strana - pocitadlo * posun)
        koniec_oranzova = min(strana, 2 * strana - pocitadlo * posun)
        pero.forward(zaciatok_oranzova)
        obdlznik(koniec_oranzova - zaciatok_oranzova, strana, 'orange')
        pero.backward(zaciatok_oranzova)
        pero.penup()
        pero.forward(strana * 1.2)

Kompletné riešenie tejto úlohy je uvedené v súbore fazy_mesiaca1.py, na ktorého odkaz je uvedený hore na tejto webovej stránke.

Táto úloha je zameraná na:

• použitie stratégií riešenia problémov - nakreslenie obrázku, dekompozícia problému na podproblémy, hľadanie vzoru,

• precvičenie príkazov volania funkcií s parametrami bez výstupu, cyklu for, korytnačej grafiky, použitie matematických výpočtov.

Vaše zaujímavé riešenia a najčastejšie chyby

Do riešenia tejto úlohy sa zapojilo 7 tímov z kategórie EXPERT. Plný počet bodov za svoje riešenie dosiahol tím pirohy_expert, ktorému srdečne  gratulujeme. Všetky tímy vyriešili úlohu pre vykreslenie nanajvýš pre párny počet fáz Mesiaca.

V riešeniach sme zaregistrovali nasledovné nedostatky, vychádzajúce najčastejšie z nedôslednej analýzy problému:

• vyriešenie úlohy len pre jeden špeciálny prípad počtu fáz,

• zbytočné vykreslenie fázy nov na začiatku aj na konci, resp. nevykreslenie jednej fázy,

• nepresné vykreslenie fáz v prvej či druhej časti, ktoré neamli byť identické ale zrkadlovo otočené,

• zle vypočítané presuny pri kreslení oranžových obdĺžnikov,

• vytvorenie funkcie bez parametra,

• namiesto použitia funkcie uvedený program ako neprehľadná sekvencia niekoľkých stoviek riadkov.