PALMA junior
Úloha o paličkových schodoch

Autorské riešenie
[stiahni py, py]

• Počet riešiteľov: 44 / 88 =  50.00 %

• Úspešnosť riešenia: 4.94 / 6 = 82.31 %

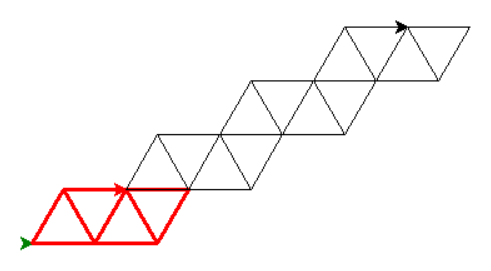
Z obrázkov zo zadania je zrejmé, že uvedené dva plániky schodov sa líšia počtom schodov a veľkosťou schodov (dĺžkou paličiek). Našou úlohou je teda naprogramovať funkciu kresli() s dvomi parametrami - počtom schodov a veľkosťou schodov.

Poďme najprv premyslieť postup ako nakreslíme jeden schod. Veľmi užitočnou pomôckou pre nás je obrázok so schodmi a zvýrazneným jedným schodom.

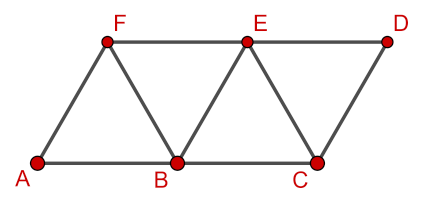
Existuje viacero možností ako vykresliť jeden schod tak, aby sme sa dostali z počiatočnej pozície kreslenia jedného schodu do počiatočnej pozície kreslenia nasledovného schodu. Označme si A, B, C, D, E, F dôležité body  v útvare tvoriacom jeden schod.

Schod môže byť vykreslený rôznymi lomenými čiarami začínajúcimi v bode A a končiacimi v bode E, napr.

• ABFAFBEFBCEBECDE (štyri trojuholníky, 15 presunov pera)

• ABEFAFBCDEBECE (dva kosoštvorce, 13 presunov pera)

• ABCDEFAFBECE (obvod a potom vnútro schodu, 11 presunov pera)

Funkcia kresli_schod() na vykreslenie jedného schodu podľa ostatného uvedeného postupu s 11 presunmi pera môže vyzerať nasledovne:

def kresli_schod(dlzka):
    for _ in range(2):
        pero.forward(2 * dlzka)
        pero.left(60)
        pero.forward(dlzka)
        pero.left(120)
    pero.left(60)
    for _ in range(2):
        pero.forward(dlzka)
        pero.right(120)
        pero.forward(dlzka)
        pero.left(120)
    pero.right(120)
    pero.backward(dlzka)
    pero.left(60)

import turtle


def posun_na_zaciatok(pocet, dlzka):
    for _ in range(pocet):
        pero.backward(dlzka)
        pero.left(60)
        pero.backward(dlzka)
        pero.right(60)


def kresli_schod(dlzka):
    for _ in range(2):
        pero.forward(2 * dlzka)
        pero.left(60)
        pero.forward(dlzka)
        pero.left(120)
    pero.left(60)
    for _ in range(2):
        pero.forward(dlzka)
        pero.right(120)
        pero.forward(dlzka)
        pero.left(120)
    pero.right(120)
    pero.backward(dlzka)
    pero.left(60)


def kresli(pocet, dlzka):
    for _ in range(pocet):
        kresli_schod(dlzka)
    posun_na_zaciatok(pocet, dlzka)


pero = turtle.Turtle()
plocha = turtle.Screen()
kresli(4, 50)
plocha.mainloop()

Priebeh vykresľovania schodov podľa uvedeného programu zachycuje nasledovná animácia:

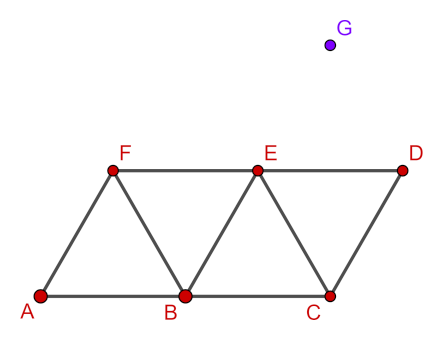
Pri uvedenom spôsobe vykreslenia jedného schodu sme dvakrát prešli po úsečkách AF a CE. Dá sa vytvoriť ešte lepšie riešenie s menším počtom presunov pera? Útvar ABCDEF obsahuje 9 úsečiek (paličiek). Ten sa dá vykresliť jedným ťahom lomenou čiarou  s počiatkom v bode F a koncom v bode C, resp. naopak (FABFEBCEDC). Pri presunutí sa z bodu C na začiatok vykreslenia nasledovného schodu do bodu G je možné sa presunúť cez vrchol E resp. D o vzdialenosť 2 paličiek alebo priamo o vzdialenosť √3 násobok dĺžky paličky.

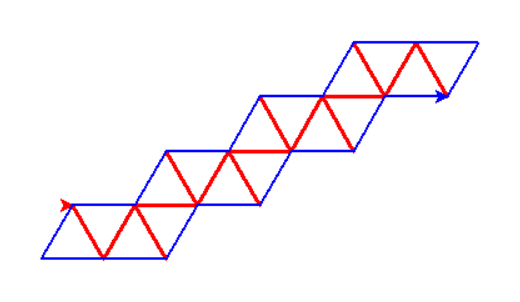
Pri vykresľovaní schodov skôr uvedenými spôsobmi si môžeme všimnúť, že pri vykresľovaní susedných schodov zbytočne prechádzame tou istou úsečkou ED. Ak sa tomu chceme vyhnúť, môžeme vykresľovať schody tak, že najprv vykreslíme ich vnútro (červená farba) a potom ich obvod (modrá farba) ako je to uvedené na obrázku nižšie.

import turtle


def vnutro_vzad(dlzka):
    pero.backward(dlzka)
    pero.right(60)
    pero.forward(dlzka)
    pero.left(60)
    pero.backward(dlzka)


def vnutro_vpred(dlzka):
    pero.forward(dlzka)
    pero.left(60)
    pero.backward(dlzka)
    pero.right(60)
    pero.forward(dlzka)


def cikcak(pocet, dlzka):
    for _ in range(pocet):
        pero.forward(dlzka)
        pero.left(60)
        pero.forward(dlzka)
        pero.right(60)


def kresli(pocet, dlzka):
    pero.left(120)
    for _ in range(pocet - 1):
        vnutro_vzad(dlzka)
        vnutro_vpred(dlzka)
    vnutro_vzad(dlzka)
    pero.right(60)
    pero.forward(dlzka)
    pero.left(120)
    pero.forward(dlzka)
    cikcak(pocet, dlzka)
    pero.left(180)
    pero.forward(dlzka)
    cikcak(pocet - 1, dlzka)
    pero.forward(dlzka)


pero = turtle.Turtle()
plocha = turtle.Screen()
kresli(4, 50)
plocha.mainloop()

Priebeh vykresľovania schodov podľa uvedeného programu zachycuje nasledovná animácia:

Uvedené riešenia sa líšili rôznym počtom presunov pera, a to:

Táto úloha je zameraná na:

• použitie stratégií riešenia problémov - nakreslenie obrázku, dekompozícia problému na podproblémy, hľadanie vzoru,

• precvičenie príkazov volania funkcií s parametrami bez výstupu, cyklu for, korytnačej grafiky.

Vaše zaujímavé riešenia a najčastejšie chyby

Do riešenia tejto úlohy sa zapojilo 29 tímov z kategórie GURU a 15 tímov z kategórie EXPERT. Plný počet bodov za svoje riešenie dosiahlo až 21 tímov, ktorým gratulujeme. Obzvlášť oceňujeme riešenie tímu file-open, ktoré vyriešilo úlohu pre ľubovoľné veľkosti dĺžok paličiek tvoriacich trojuholníkovú konštrukciu schodov či tímu roboram za riešenie úlohy s rôzne zadanou šírkou a výškou schodu, a tiež riešenia tímov oliverseman a mongomongosh za použitie komentárov a spracovanie výnimiek.

V 39 riešeniach súťažiaci použili korytnačiu grafiku a len v 5 riešeniach karteziánsku grafiku. V jednom riešení súťažiaci na vykresľovanie schodov použili naraz 2 korytnačky.

V riešeniach sme zaregistrovali nasledovné nedostatky, vychádzajúce najčastejšie z nedôslednej analýzy problému:

• vytvorenie funkcie kresli() bez parametrov alebo len s jedným parametrom - počtom poschodí a s pevnou alebo náhodnou veľkosťou schodu (paličky),

• zbytočné viacnásobné prechody pri vykresľovaní niektorých úsečiek, prípadne aj prefarbovanie úsečiek bielou farbou (ako mazanie nechcených úsečiek),

• vykreslenie iného typu schodov ako boli požadované v zadaní úlohy,

•  zlá dekompozícia riešenia, keď sa pri zadaní parametra počtu schodov 0 vykreslí schod alebo časť schodu,

• chybné určenie počtu úsečiek (paličiek) v závislosti od počtu schodov,

• ak sa programovom kóde používajú absolútne natočenia s relatívnymi posunmi pera, znemožní to použiť riešenie pri vykreslení schodov pri ľubovoľnom počiatočnom natočení pera,

• v Pythone sa odporúča písať na začiatku programového kódu importy, funkcie a až po nich kód hlavného programu,

• rovnako sa odporúča používať prirodzené názvy premenných, napr. "veľkosť", "dĺžka", "počet_schodov", nie nič nehovoriace jedno-písmenové názvy ako napr. "a", "b".