PALMA junior
Úloha o obrázkovom darčeku

Autorské riešenie
[stiahni py, py]                                      

• Počet riešiteľov: 14 / 14 = 100 %

• Úspešnosť riešenia: 5,49 / 7 = 78,37 %

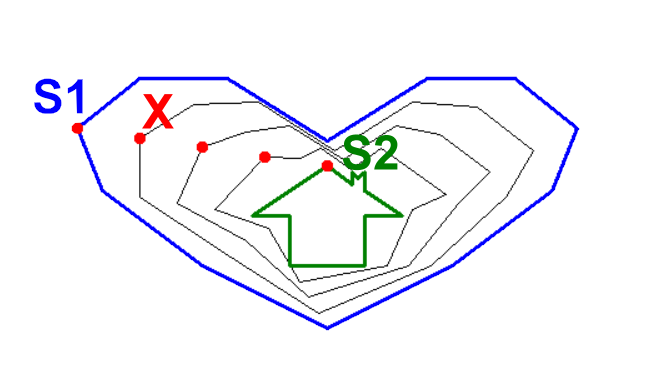
Cieľom úlohy je vykresliť obrázok pozostávajúci z dvoch okrajových symbolov a prechodových vrstiev medzi týmito symbolmi.

Obidva okrajové symboly sú tvorené lomenými čiarami s rovnakým počtom uzlových bodov. V každom symbole je prvý bod symbolu totožný s posledným bodom symbolu.

Pri vykresľovaní každej vnútornej vrstvy obrázku medzi okrajovými symbolmi potrebujeme vypočítať súradnice každého uzlového bodu danej vnútornej vrstvy.

Súradnice uzlového bodu X vypočítame zo súradníc odpovedajúcich uzlových bodov oboch symbolov S1 a S2, poradia vrstvy PORADIE a počtu vrstiev POČET.

Bod X, leží na spojnici bodov S1 a S2. Vektor X-S1 je K násobkom vektora S2-S1, čo zapíšeme:

X - S1 = K * (S2 - S1)

Tento zápis pre vektory môžeme prepísať na zápis pre body:

X = S1 + K * (S2 - S1)

Pre K = 0 dostaneme X = S1 a, pre K = 1 dostaneme X = S2.

Ak máme zadaný počet vrstiev ako premennú POČET a poradie vrstvy ako premennú PORADIE (nadobúdajúcu postupne hodnoty 0 až POČET-1), tak koeficient K vypočítame ako podiel:

K = PORADIE / (POČET - 1)

 Po dosadení koeficietu K do predchádzajúceho zápisu, dostaneme zápis pre výpočet súradníc uzlového bodu X vrstvy s poradím PORADIE pre zadaný počet vrstiev POČET a pre odpovedajúce súradnice uzlových bodov S1 a S2 oboch symbolov:

  X = S1 + PORADIE / (POČET - 1) * (S2 - S1)

Tento vzťah použijeme pri vypočte všetkých uzlových bodov lomených čiar pre každú vrstvu.

Funkcia vytvor_vrstvu() na vytvorenie zoznamu súradníc novej vrstvy pre zadané zoznamy súradníc okrajových symbolov v parametroch utvar_1 a utvar_2, poradie vrstvy v parametri poradie a počtu vrstiev v parametri pocet môže vyzerať nasledovne:

def vytvor_vrstvu(utvar_1, utvar_2, poradie, pocet):
    utvarx = []
    for idx in range(len(utvar_1)):
        x = utvar_1[idx][0] + \
            poradie / (pocet - 1) * (utvar_2[idx][0] - utvar_1[idx][0])
        y = utvar_1[idx][1] + \
            poradie / (pocet - 1) * (utvar_2[idx][1] - utvar_1[idx][1])    
        utvarx.append([x, y])
    return utvarx       

Funkcia kresli_vrstvu() na vykreslenie vrstvy tvorenej zoznamom súradníc v parametri utvar a hrúbkou pera v parametri hrubka môže vyzerať nasledovne:

def kresli_vrstvu(utvar, hrubka):
    pero.pensize(hrubka)
    pero.penup()
    pero.setposition(utvar[0][0], utvar[0][1])
    pero.pendown()
    for idx in range(1, len(utvar)):
        pero.setposition(utvar[idx][0], utvar[idx][1])      

V tejto funkcii je dôležité sa presunúť do prvého bodu útvaru so zdvihnutým perom a presuny do ďalších bodov lomenej čiary robiť s položeným perom.

Funkcia kresli() na vykreslenie všetkých vrstviev medzi okrajovými vrstvami, ktorých súradnice sú v parametroch utvar_1 a utvar_2 a počet vrstiev v parametri  pocet môže vyzerať nasledovne:

def kresli(utvar_1, utvar_2, pocet):
    for poradie in range(pocet):
        utvar = vytvor_vrstvu(utvar_1, utvar_2, poradie, pocet)
        if poradie == 0 or poradie == pocet - 1:
            kresli_vrstvu(utvar, 3)
        else:
            kresli_vrstvu(utvar, 1)     

V tejto funkcii v cykle vypočítavame súradnice aktuálnej vrstvy a následne ju vykreslíme. Pri prvej a poslednej vrstve nastavíme hrúbku pera na 3 pri vnútorných vrstvách je hrúbku pera rovná 1.

Výsledné riešenie úlohy v jazyku Python s použitím modulu turtle môže vyzerať nasledovne:

#Python
import turtle


def vytvor_vrstvu(utvar_1, utvar_2, poradie, pocet):
    utvarx = []
    for idx in range(len(utvar_1)):
        x = utvar_1[idx][0] + \
            poradie / (pocet - 1) * (utvar_2[idx][0] - utvar_1[idx][0])
        y = utvar_1[idx][1] + \
            poradie / (pocet - 1) * (utvar_2[idx][1] - utvar_1[idx][1])
        utvarx.append([x, y])
    return utvarx


def kresli_vrstvu(utvar, hrubka):
    pero.pensize(hrubka)
    pero.penup()
    pero.setposition(utvar[0][0], utvar[0][1])
    pero.pendown()
    for idx in range(1, len(utvar)):
        pero.setposition(utvar[idx][0], utvar[idx][1])


def kresli(utvar_1, utvar_2, pocet):
    for poradie in range(pocet):
        utvar = vytvor_vrstvu(utvar_1, utvar_2, poradie, pocet)
        if poradie == 0 or poradie == pocet - 1:
            kresli_vrstvu(utvar, 3)
        else:
            kresli_vrstvu(utvar, 1)


tabula = turtle.Screen()
tabula.delay(0)
pero = turtle.Turtle()
pero.hideturtle()

symbol_1 = [[0, 0], [100, 50], [180, 110], [200, 160], [150, 200], 
            [80, 200], [0, 150], [-80, 200], [-150, 200], [-200, 160], 
            [-180, 110], [-100, 50], [0, 0]]
symbol_2 = [[-30, 50], [30, 50], [30, 90], [60, 90], [30, 110], 
            [30, 125], [25, 120], [20, 125], [20, 115], [0, 130], 
            [-60, 90], [-30, 90], [-30, 50]]
pocet_vrstiev = 5

kresli(symbol_1, symbol_2, pocet_vrstiev)

tabula.mainloop()

Trochu kratšie riešenie môžeme vytvoriť použitím modulu tkinter, v ktorom vieme použiť metódu create_polygon na vykreslenie lomenej čiary. V tomto "počítačovom" súradnicovom systéme súradnica x nadobúda hodnoty od 0 vyššie a súradnica y nadobúda hodnoty od 0 vyššie, ale smerom nadol. Tento fakt treba brať do úvahy pri navrhovaní symbolov. 

Výsledné riešenie úlohy v jazyku Python s použitím modulu tkinter môže vyzerať nasledovne:

#Python
import tkinter


def vytvor_vrstvu(utvar_1, utvar_2, poradie, pocet):
    utvarx = []
    for idx in range(len(utvar_1)):
        x = utvar_1[idx][0] + \
            poradie / (pocet - 1) * (utvar_2[idx][0] - utvar_1[idx][0])
        y = utvar_1[idx][1] + \
            poradie / (pocet - 1) * (utvar_2[idx][1] - utvar_1[idx][1])
        utvarx.append([x, y])
    return utvarx


def kresli(utvar_1, utvar_2, pocet):
    for poradie in range(pocet):
        utvar = vytvor_vrstvu(utvar_1, utvar_2, poradie, pocet)
        if poradie == 0 or poradie == pocet - 1:
            platno.create_polygon(utvar, outline='black', fill='', width=3)
        else:
            platno.create_polygon(utvar, outline='black', fill='', width=1)


okno = tkinter.Tk()
okno.title('Obrázkový darček')
platno = tkinter.Canvas(okno, height=600, width=600)
platno.grid()

symbol_1 = [[300, 300], [400, 250], [480, 190], [500, 140], [450, 100], 
            [380, 100], [300, 150], [220, 100], [150, 100], [100, 140], 
            [120, 190], [200, 250], [300, 300]]

symbol_2 = [[270, 250], [330, 250], [330, 210], [360, 210], [330, 190], 
            [330, 175], [325, 180], [320, 175], [320, 185], [300, 170], 
            [240, 210], [270, 210], [270, 250]]

pocet_vrstiev = 5

kresli(symbol_1, symbol_2, pocet_vrstiev)

okno.mainloop()

Táto úloha je zameraná na:

• použitie stratégie riešenia problémov - dekompozície problému na podproblémy,

• dôslednú analýzu riešenia úlohy,

• precvičenie príkazov volania funkcií s parametrami a výstupom, práce so zoznamami, výpočtov so súradnicami (lineárna interpolácia), príkazov opakovania a vetvenia,

• grafickú tvorivosť pri návrhu vlastných obrázkov s okrajovými symbolmi.

Vaše zaujímavé riešenia a najčastejšie chyby

Do riešenia úlohy sa zapojilo 14 súťažných tímov. Plný počet bodov za riešenie tejto úlohy získali 4 tímy albatros, elemejou, file-open, sigma, ktorým gratulujeme. Chválime tím bonkpro za ošetrenie vstupov a tímy sigma, zirafky a invalidne rakety za viaceré originálne návrhy obrázkov. V súťažných riešeniach 8 tímov použilo modul tkinter a 6 tímov modul turtle.

V riešeniach sme zaregistrovali nasledovné nedostatky, vychádzajúce najčastejšie z nedôslednej analýzy problému:

• nesprávny počet vykreslených vrstiev - niektorí vykreslili o 1, iní o 2 vrstvy navyše, než boli uvedené vo volaní funkcie kresli(),

• vykresľovanie nadbytočných čiar medzi vrstvami - chcelo to zvihnúť pero pri presune na novú vrstvu,

• pri vykresľovaní okrajových vrstviev ich nezvýraznenie väčšou hrubkou pera oproti vnútorným vrstvám,

• nesprávny vzťah na výpočet vykreslenia bodov jednotlivých vnútorných vrstviev,

• nepoužitie funkcíí,

• absencia originálnych symbolov alebo nepostačujúce testovacie dáta (napr. s podprahovým počtom uzlových bodov ako sa to vyžadovalo v zadaní).