PALMA junior
Úloha o neurónových sieťach

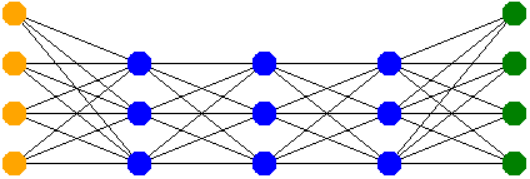
Autorské riešenie
[stiahni py]                                       

• Počet riešiteľov: 20 / 20 = 100 %

• Úspešnosť riešenia:  5,95 / 7 = 85 %                   

Pri riešení tejto úlohy sa musíme zamyslieť, čo je najdôležitejšou časťou programu. Na to, aby sme dosiahli úspešne riešenie musíme správne vypočítať súradnice umiestnenia neurónov a takto aj súradnice prepojení medzi nimi a medzi jednotlivými vrstvami. Musíme si uvedomiť, že pri vykresľovaní, či už neurónov alebo prepojení, treba myslieť aj na to, aký bude rozostup medzi jednotlivými neurónmi a vrstvami a akou farbou budeme neuróny vykresľovať. Začneme tou jednoduchšou časťou a to vykresľovaním neurónov.

Neurónová sieť má na vstupnej vrstve oranžové neuróny, na skrytej vrstve modré a na výstupnej vrstve zelené.

Vykreslenie neurónov
Pri vykresľovaní neurónov na jednej vrstve si musíme najprv určit, kde sa bude táto vrstva nachádzať - teda jej x-ovú súradnicu. Podľa počtu neurónov, ktoré chceme na tejto vrstve vykresliť prechádzame for-cyklom v ktorom, vykreslíme neurón na zadanej x-ovej a y-ovej súradnici. Následne sa posunieme dopredu o určený rozostup, kde opäť vykreslíme neurón, atď. X-ová súradnica sa nemení, tá určuje pozíciu vrstvy. Mení sa y-ová súradnica, ktorá určuje pozíciu neurónu vo vrstve. Priemer neurónu si môžeme určiť napríklad o veľkosti polovičnej dĺžky rozostupu.

def kresli_neurony(pocet, x_sur, farba, rozostup):
    for i in range(pocet):
        pero.goto(x_sur, i * rozostup)
        pero.dot(rozostup / 2, farba)
                

Vykreslenie prepojení
Ak už vieme ako vykresľovať neuróny vo vrstve, tak teraz ich musíme prepojiť. Každý neurón na jednej vrstve má byť prepojený s každým neurónom na nasledujúcej vrstve. Potrebujeme teda poznať x-ové a y-ové súradnice obidvoch vrstiev - počiatočnej a nasledujúcej. Teda z x-ovej a y-ovej súradnice neurónu počiatočnej vrstvy vytvoríme prepojenie na všetky neuróny z nasledujúcej vrstvy. Už vieme, že neuróny sú od seba vzdialené o rozostup.

def kresli_spojnice(pocet_start, x_sur_start, pocet_koniec, x_sur_koniec, rozostup):
    for y_start in range(pocet_start):
        for y_koniec in range(pocet_koniec):
            pero.goto(x_sur_start, y_start * rozostup)
            pero.pendown()
            pero.goto(x_sur_koniec, y_koniec * rozostup)
            pero.penup()
            

Vykreslenie neurónovej siete
Spojením týchto dvoch funkcii vytvoríme vykreslenie neurónovej siete.
Začneme prvou vrstvou - určíme si x-ovú súradnicu vstupnej vrstvy nech je 0 a rozostup medzi neurónmi a vrstvami nech je 70. Vykreslíme spojnice medzi vstupnou vrstvou a prvou skrytou vrstvou. Následne vykreslíme neuróny vstupnej vrstvy.
Pri kreslení každej ďalšej vrstvy zväčšíme hodnotu x-ovej súradnice o rozostup. Podľa počtu skrytých vrstiev prejdeme for-cyklom a vykreslíme spojenia medzi všetkými skrytými vrstvami okrem poslednej. Následne vykreslíme neuróny skrytých vrstiev. Posledná skrytá vrstva sa prepája s výstupnou vrstvou. Teda prechádzame for-cyklom o 1 menej krát ako je počet skrytých vrstiev.
Po prejdení for-cyklom vykreslíme spojenia medzi poslednou skrytou vrstvou a výstupnou vrstvou. Ako posledný krok vykreslíme neuróny výstupnej vrstvy. Pri taktomto uvažovaní by nasledujúci kód vyzeral nasledovne.

def neuronova_siet_1(vstupna, pocet_skryte, skryta, vystupna):
    xova = 0
    rozostup = 70
    pero.penup()
    kresli_spojnice(vstupna, xova, skryta, rozostup, rozostup)
    kresli_neurony(vstupna, xova, "orange", rozostup)
    xova = xova + rozostup

    for i in range(1, pocet_skryte):
        kresli_spojnice(skryta, xova, skryta, xova + rozostup, rozostup)
        kresli_neurony(skryta, xova, "blue", rozostup)
        xova = xova + rozostup

    kresli_spojnice(skryta, xova, vystupna, xova + rozostup, rozostup)
    kresli_neurony(skryta, xova, "blue", rozostup)

    xova = xova + rozostup
    kresli_neurony(vystupna, xova, "green", rozostup)

Túto úlohu je možné riešiť podobným, viac úhľadnejším spôsobom. Použijeme dátovú štruktúru neurony_vo_vrstvách, ktorá obsahuje počet všetkých neurónov, ktoré budú v našej sieti. Je taktiež prehľadnejšie, ak rozlišujeme rozostup medzi neurónmi na jednej vrstve a rozostup medzi jednotlivými vrstvami. V tomto prípade vykreslíme naraz všetky prepojenia a to tak, že prechádzame for-cyklom toľko krát, koľko je počet všetkých neurónov. Pomocou indexov tohto poľa získame súradnice na vykreslenie prepojení a takisto na nasledovné vykreslenie neurónov. Kód takéhoto riešenia je nasledovný.

#Python

import turtle

def kresli_neurony(pocet, x_sur, farba, rozostup):
    for i in range(pocet):
        pero.goto(x_sur, i * rozostup)
        pero.dot(rozostup / 2, farba)

def kresli_spojnice(pocet_start, x_sur_start, pocet_koniec, x_sur_koniec, rozostup):
    for y_start in range(pocet_start):
        for y_koniec in range(pocet_koniec):
            pero.goto(x_sur_start, y_start * rozostup)
            pero.pendown()
            pero.goto(x_sur_koniec, y_koniec * rozostup)
            pero.penup()

def neuronova_siet_2(pocet_neurony_vstup, 
                     pocet_neurony_vnutro,
                     pocet_vrstvy_vnutro,
                     pocet_neurony_vystup):
    rozostup_vrstiev = 100
    rozostup_neuronov = 40
    neurony_vo_vrstvach = [pocet_neurony_vstup] + \
                          [pocet_neurony_vnutro] * pocet_vrstvy_vnutro + \
                          [pocet_neurony_vystup]
    
    for idx in range(len(neurony_vo_vrstvach) - 1):
        kresli_spojnice(neurony_vo_vrstvach[idx], 
                        idx * rozostup_vrstiev,
                        neurony_vo_vrstvach[idx + 1], 
                        (idx + 1) * rozostup_vrstiev, 
                        rozostup_neuronov)

    for idx in range(len(neurony_vo_vrstvach)):
        if idx == 0:
            farba = 'orange'
        elif idx < len(neurony_vo_vrstvach) - 1:
            farba = 'blue'
        else:
            farba = 'green'
        kresli_neurony(neurony_vo_vrstvach[idx], 
                       idx * rozostup_vrstiev, 
                       farba, 
                       rozostup_neuronov)

Vaše zaujímavé riešenia a najčastejšie chyby

Všetci úspešní riešitelia postupovali podobne ako v autorskom riešení. V niektorých prípadoch sa súradnice nevypočítavali v samostatných funkciách ale spolu v jednej funkcii sa vypočítali súradnice a následne aj vykreslili neuróny a prepojenia. Ak sa vyskytli chyby, tak sa väčšinou týkali nesprávneho výpočtu súradníc neurónov alebo prepojení. Niektorí riešitelia vykreslili viac alebo menej prepojení ako mali alebo spájali neuróny na jednej vrstve, čo nebolo potrebné. V niekoľkých prípadoch riešitelia najprv vykreslili neuróny a až následne prepojenia, takto riešenie nebolo nesprávne, no úhľadnejšie by to bolo v opačnom poradí.