PALMA junior
Úloha o pečení koláčikov

Autorské riešenie
[stiahni py, py]

• Počet riešiteľov: 9 / 9 = 100 %

• Úspešnosť riešenia: 3,33 / 5 =  66,6 %

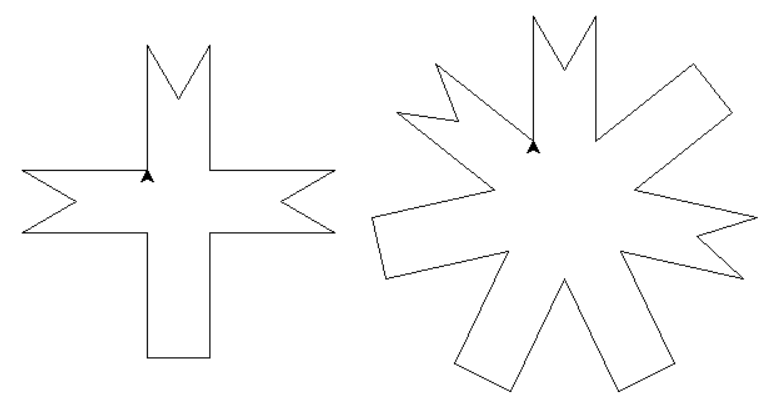
Podľa zadania úlohy sú špeciálne koláčiky tvorené zadaným počtom náhodne rozmiestnených ramien dvoch typov.

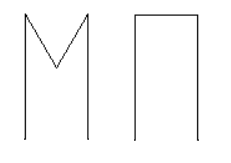
Prvý typ ramena (vykrojený) pripomína tvar písmena M a druhý typ ramena (nevykrojený) pripomína tvar gréckeho písmena Pí.

Na vykreslenie jednotlivých ramien využijeme funkcie m_rameno a pi_rameno, v ktorých použijeme príkazy korytnačej grafiky forward, right, left s patričnými hodnotami.

# Python
def m_rameno(dlzka):
    pero.forward(dlzka)
    pero.right(150)
    pero.forward(dlzka / 2)
    pero.left(120)
    pero.forward(dlzka / 2)
    pero.right(150)
    pero.forward(dlzka)
    pero.right(180)


def pi_rameno(dlzka):
    pero.forward(dlzka)
    pero.right(90)
    pero.forward(dlzka / 2)
    pero.right(90)
    pero.forward(dlzka)
    pero.right(180)

Pre vykreslenie koláčika so zadaným počtom oboch typov ramien s ich náhodným rozmiestnením vytvoríme funkciu kresli_kolacik, ktorá bude využívať funkcie m_rameno a pi_rameno.

Ak by sme chceli vykresliť koláčik bez použitia náhody, tak by sme najprv vykreslili zadaný počet ramien tvaru písmena M a potom zadaný počet ramien tvaru písmena Pí. My však podľa zadania máme vykresliť zadaný počet ramien oboch typov s náhodným rozmiestnením. Jedným z riešením je použiť pomocné premenné pocitadlo_m a pocitadlo_pi, pomocou ktorých si zapamätáme aktuálny počet vykreslených ramien oboch typov. Potom v cykle budeme hádzať mincou a podľa jej hodnoty, ak to bude možné, zvýšime prvé alebo druhé počítadlo a vykreslíme rameno jedného typu, a ak to nebude možné tak rameno druhého typu.  

Celkové riešenie úlohy môže vyzerať nasledovne:

# Python
import turtle
import random


def m_rameno(dlzka):
    pero.forward(dlzka)
    pero.right(150)
    pero.forward(dlzka / 2)
    pero.left(120)
    pero.forward(dlzka / 2)
    pero.right(150)
    pero.forward(dlzka)
    pero.right(180)


def pi_rameno(dlzka):
    pero.forward(dlzka)
    pero.right(90)
    pero.forward(dlzka / 2)
    pero.right(90)
    pero.forward(dlzka)
    pero.right(180)


def kresli_kolacik(dlzka, pocet_m, pocet_pi):
    pocitadlo_m = 0
    pocitadlo_pi = 0
    pero.left(90)
    for i in range(pocet_m + pocet_pi):
        rameno = random.randint(0, 1)
        if (rameno == 0):
            if (pocitadlo_m < pocet_m):
                m_rameno(dlzka)
                pocitadlo_m = pocitadlo_m + 1
            else:
                pi_rameno(dlzka)
                pocitadlo_pi = pocitadlo_pi + 1
        else:
            if (pocitadlo_pi < pocet_pi):
                pi_rameno(dlzka)
                pocitadlo_pi = pocitadlo_pi + 1
            else:
                m_rameno(dlzka)
                pocitadlo_m = pocitadlo_m + 1

        pero.right(360 / (pocet_m + pocet_pi))


pero = turtle.Turtle()
tabula = turtle.Screen()

kresli_kolacik(100, 3, 2)

tabula = turtle.mainloop()

Túto úlohu možeme vyriešiť aj pomocou zoznamu. Tento zoznam bude na začiatku obsahovať čísla 0 a 1. Počet prvkov 0 v zozname bude odpovedať počtu ramien typu M a počet prvkov 1 počtu ramien typu Pí. Premiešaním prvkov zoznamu (pomocou funkie shuffle) dostaneme zoznam s náhodným rozmiestnením 0 a 1 s ich odpovedajúcim zastúpením. Potom riešenie úlohy bude pomerne jednoduché, kde v cykle postupne vykresľujeme podľa jednotlivých hodnôt zoznamu jeden alebo druhý typ ramena. Výsledná funkcia kresli_kolacik môže vyzerať nasledovne:

# Python
def kresli_kolacik(dlzka, pocet_m, pocet_pi):
    poradie_kolacikov = pocet_m * [0] + pocet_pi * [1]
    random.shuffle(poradie_kolacikov)
    for typ_kolacika in poradie_kolacikov:
        if typ_kolacika == 0
            m_rameno(dlzka)
        else:
            pi_rameno(dlzka)
        pero.right(360 / len(poradie_kolacikov))

Táto úloha je zameraná na:

• použitie stratégie riešenia problémov - dekompozície problému na podproblémy,

• precvičenie príkazov volania funkcií s parametrom, príkazov opakovania a vetvenia, príkazov korytnačej grafiky

• a v prípade druhého riešenia aj na precvičenia práce s dátovým typom zoznam a funkcie shuffle.

Vaše zaujímavé riešenia a najčastejšie chyby

Do riešenia tejto úlohy sa zapojilo 9 tímov z kategórie EXPERT. Plný počet bodov dosiahli tímy oliverseman, mangomongosh, byg expert, bazosaci, ktorým gratulujeme.

Najčastejšou chybou žiackych riešení bolo, že riešitelia pri vstupe neodlišovali počet ramien tvaru M a počet ramien tvaru Pí. Použili iba jednu premennú - počet ramien dokopy a potom už náhodne vyberali ich poradie a počet typov ramien.

S náhodným generovaním problém nebol v žiadnom riešením okrem jedného, kde riešiteľ zakódoval typy ramien ako 0 a 1. Pri príkaze spustenia metódy ako vstup zadal "kresli_kolacik("110100110")". Takže vlastne negeneroval nič náhodne.

V inom prípade riešiteľ pevne určil počet ramien na 10. Teda, aj napevno vypočítal uhol medzi ramenami, takže pre akýkoľvek iný počet ramien toto riešenie nebolo funkčné.