PALMA junior
Úloha o stabilite vežičky zostavenej z kociek

Autorské riešenie
[stiahni py]

• Počet riešiteľov: 11 / 11 = 100,00 %

• Úspešnosť riešenia: 3,63 / 7 = 51,82 %

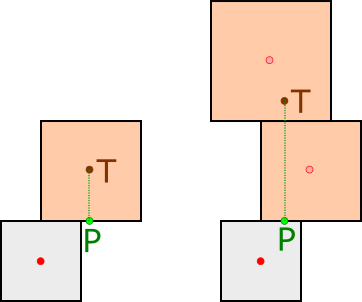
Pri riešení tejto úlohy nám pomôže rozbor konkrétneho prípadu zo zadania úlohy. Vežička zostavená z troch kociek s rozmermi a posunmi [[12, 1], [10, 5], [8, 0]] je stabilná, lebo priemet P ťažiska T telesa zloženého z dvoch horných kociek leží na hornej hrane spodnej kocky. Ak uvažujeme vežičku bez hornej kocky s rozmermi a posunmi [[10, 5], [8, 0]], tak tá je nestabilná, lebo priemet P ťažiska T vrchnej kocky leží mimo hornú hranu spodnej kocky. Presvedčíme sa o tom nasledovným výpočtom.

V prípade telies s rovnakou hustotou, môžeme pre výpočet x-ovej súradnice ťažiska sústavy dvoch telies namiesto vzťahu s hmotnosťami

x_t  = (x_t1 * m₁ + x_t2 * m₂) / (m₁ + m₂)

použiť vzťah s objemami telies, t.j.

x_t  = (x_t1 * V₁ + x_t2 * V₂) / (V₁ + V₂)

Pri použití tohto vzťahu na sústavu viacerých telies (kociek) musíme testovať či sú stabilné všetky sústavy zhora prvých 2, 3, ... n kociek.

Výsledné riešenie úlohy zapísané v programovacom jazyku Python môže vyzerať nasledovne:

def je_stabilna(vezicka):
    # inicializácia x-posunu a objemu telesa 
    # (x_nad, objem_nad) umiestneného nad skúmanou kockou
    veza = vezicka.copy()
    a, x_nad = veza.pop(0)
    objem_nad = a ** 3
    # zisťovanie či teleso z kociek (x_nad, objem_nad) je stabilné 
    # nad aktuálne skúmanou kockou
    for a, x in veza:
        # zistenie či priemet ťažiska telesa z kociek (x_nad), 
        # leží na hornej podstave skúmanej kocky
        stabilna = x - a / 2 <= x_nad <= x + a / 2
        if not stabilna:
            return False
        # výpočet rozmerov nového telesa rozšíreného o skúmanú kocku - 
        # pre ďalšiu iteráciu cyklu
        objem = a ** 3
        x_nad = (objem_nad * x_nad + objem * x) / (objem_nad + objem)
        objem_nad = objem_nad + objem
    return stabilna


# ilustračný príklad
print(je_stabilna([[12, 1], [10, 5], [8, 0]])) 

# ilustračný príklad bez hornej kocky
# print(je_stabilna([[10, 5], [8, 0]])) 

# prípad, keď 3D veža je nestabilná a 2D je stabilná
# print(je_stabilna([[2, -1], [1, -0.5], [1.8, 0]])) 

Táto úloha je zameraná na: 

• použitie rôznych stratégii riešenia problémov (dekompozície problému na podproblémy, vykreslenie obrázka),

• precvičenie príkazov opakovania, vetvenia s podmienkou, volania funkcií s parametrom a výstupom, práce s dátovým typom zoznam, výpočtov s aritmetickými a relačnými operátormi,

• aplikáciu fyzikálnych poznatkov na algoritmické vyriešenie reálneho problému.

Vaše zaujímavé riešenia a najčastejšie chyby

Do riešenia tejto úlohy sa zapojilo 11 tímov z kategórie GURU.  Plný počet bodov dosiahli tímy seesharp a BonifacGroup, ktorým gratulujeme.

V riešeniach sme zaregistrovali nasledovné nedostatky, vychádzajúce najčastejšie z nedôslednej analýzy problému, tvorby menej efektívneho riešenia či z pretrvávajúcich programátorských zlozvykov:

• pri riešení úlohy nebol vôbec použitý výpočet ťažiska,

• pri výpočte ťažiska sa namiesto objemov kociek rátali plochy štvorcov, resp. dĺžky hrán kociek,

• pri určení stability sústavy kociek bola nesprávne použitá ostrá nerovnosť,

• podmienka stability nie je správna, lebo by mala zohľadňovať polohu ťažiska sústavy kociek nad danou kockou, nie len kocky bezprostredne nad ňou,

• vyriešenie len ilustračného príkladu zo zadania,

• namiesto plnovýznamových identifikátorov premenných použitie málohovoriacich jednopísmenových identifikátorov.