PALMA junior
Úloha o aktivite srdca

Autorské riešenie
[stiahni py]                                       

• Počet riešiteľov: 7 / 8 = 88  %                       

• Úspešnosť riešenia:  4.29 / 5 = 86 %                   

Správne riešenie úlohy si vyžadovalo pozorné a starostlivé prečítanie zadania a jeho porozumenie. Riešenie úlohy totiž viedlo k úprave vstupného zoznamu hodnôt aktivity srdca tak, aby:

• nový zoznam obsahoval dvojnásobný počet hodnôt aktivity srdca,
• výsledný tvar EKG záznamu vytvorený pomocou nového zoznamu bol približne rovnaký.

Pre splnenie prvej podmienky postačí vytvoriť nový prázdny zoznam, do ktorého budeme pre každú hodnotu starého zoznamu vkladať dvojicu hodnôt:

• kópiu hodnoty starého zoznamu
• a novo-vytvorenú hodnotu pomocou hodnôt starého zoznamu.

Novú hodnotu potrebujeme vytvoriť tak, aby výsledný tvar EKG záznamu zoznam nezmenený. Jednou z možností je uvažovať priemernú hodnotu dvoch susedných prvkov. Môžeme si však predstaviť aj iné alternatívy. Napríkad ľavého alebo pravého suseda započítať s väčšou váhou, a tak rátať vážený priemer. Alebo na určenie novej hodnoty môžeme využiť aj priemer viacerých susedov. Prístup s využitím aritmetického priemeru ľavého a pravého suseda je znázornený na nasledujúcom obrázku. V hornej časti obrázka je hodnota v indexe 0 rovná 1, v indexe 1 je hodnota rovná 0,6 a tak ďalej. Všimnite si, že pomocou indexov 0,1,2,3,4,5 (6 hodnôt) v hornej časti obrázka vieme skonštruovať v dolnej časti obrázka iba hodnoty na indexoch 0-10 (čiže 11 hodnôt), a teda dvanásta hodnota nám chýba.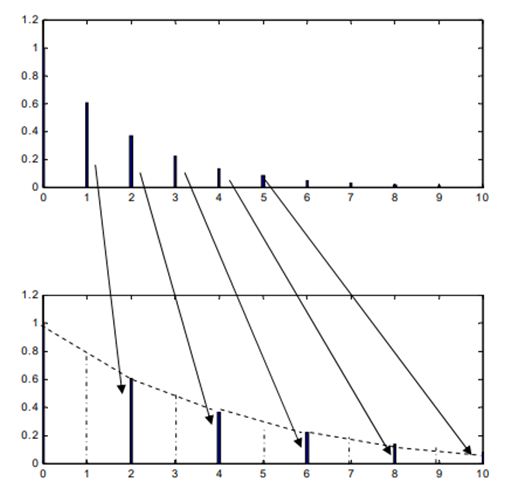

Ostáva nám teda vyriešiť otázku, ako bude vyzerať posledný (v našom prílade dvanásty, lebo číslujeme od nuly) prvok zoznamu, ktorý nemá pravého suseda. V takom prípade môžeme zachovať trend krivky - ak krivka pred posledným bodom rástla alebo klesala, tak novú hodnotu môžete nastaviť napríklad pomocou vzťahu:

pričom pod premennou priemer si môžeme predstaviť vypočítaný priemer pre poslednú možnú dvojicu susedných prvkov starého zoznamu.

Úloha teda mala viacero možných riešení, jedno z možných riešení v jazyku Python má nasledujúcu podobu:

def uprav_zaznam(zoznam: list):
    novyZoznam = []
    for i in range(len(zoznam)-1):
        novyZoznam.append(zoznam[i])
        priemer = (zoznam[i] + zoznam[i+1])/2
        novyZoznam.append(priemer)
    novyZoznam.append(zoznam[-1])
    novyZoznam.append(zoznam[-1] + novyZoznam[-1] - priemer)
    return novyZoznam

Vaše zaujímavé riešenia a najčastejšie chyby

Úlohu riešilo 7 tímov a päť z nich získalo plný počet bodov. Riešenia používali len aritmetický priemer, ale líšili sa v spôsobe určenia poslednej hodnoty nového zoznamu. Niektoré tímy využili zopakovanie posledného prvku ešte raz, niektoré na úvod zoznamu dvakrát zopakovali prvý prvok. Niektoré tímy dokonca náhodne generovali 100 prvkový zoznam hodnôt a riešenie vyhodnocovali na takomto zozname. Nepresnosti vznikali, ak ste zoznam síce zdvojnásobili a vložili na prázdne miesta nuly, ale ďalej ste už nuly neupravovali. Namiesto núl je potrebné ešte zvoliť vhodné hodnoty tak, aby sa tvar krivky nezmenil (napríklad aritmetický priemer susedov).