PALMA junior
Úloha o rýchlom výpočte kĺzavého mediánu

Autorské riešenie
[stiahni py]

• Počet riešiteľov: 7 / 8 = 88 %

• Úspešnosť riešenia: 3,57 / 7 = 51 %

Pri tejto úlohe musíme myslieť na dve veci.

1. Výpočet kĺzavého mediánu musí byť správny.

2. Výpočet kĺzavého mediánu musí byť čo najrýchlejší.

V takýchto prípadoch môžeme postupovať tak, že najskôr vytvoríme nejaké správne riešenie a potom ho budeme postupne vylepšovať (ak sa bude dať a budeme vedieť ako). Tento prístup má aj dve výhody:

1. Každé ďalšie riešenie môžeme porovnať s tým predchádzajúcim či naozaj došlo k vylepšeniu (v našom prípade k zrýchleniu).

2. Výsledky každého ďalšieho riešenia môžeme porovnať s výsledkami toho predchádzajúceho, aby sme sa uistili, že aj nové riešenie je správne.

Vytvorme si správne riešenie. Postupovať môžeme tak, ako je uvedené v zadaní:

• Hodnoty stačí usporiadať a mediánom je tá, ktorá je v strede.

• Kĺzavý medián sa počíta z postupnosti hodnôt tak, že medián vypočítame pre každú podpostupnosť zadanej dĺžky.

Vytvorme si najskôr funkciu pre výpočet mediánu v usporiadanej podpostupnosti: 

# Python
def median(podpostupnost):
    dlzka = len(podpostupnost)
    if dlzka % 2 == 0:
        return (podpostupnost[dlzka // 2 - 1] + podpostupnost[dlzka // 2]) / 2
    return podpostupnost[dlzka // 2]

Túto funkciu volajme pre jednotlivé usporiadané podpostupnosti celej postupnosti hodnôt. 

# Python
def klzavy_median_1(postupnost, dlzka):
    mediany = []
    for index in range(len(postupnost) - dlzka + 1):
        podpostupnost = postupnost[index:index + dlzka]
        podpostupnost.sort()
        mediany.append(median(podpostupnost))
    return mediany

Teraz máme funkčné a správne riešenie. Pozrime sa, či by sa nedalo nejako vylepšiť. Všimnime si, ako pracujeme s jednotlivými podpostupnosťami. Podpostupnosť usporiadame. Ďalšia podpostupnosť sa od predchádzajúcej líši len tím, že jeden prvok sme z nej odstránili  a jeden prvok sme do nej vložili. Mohli by sme teda nejako využiť to, že po odstránení prvku je podpostupnosť stále usporiadaná. Vložiť prvok do usporiadanej podpostupnosti vieme spraviť aj bez toho, aby sme ju nanovo usporadúvali. Pozíciu vkladaného prvku vieme nájsť priamo. Postupovať môžeme takto:

1. Ak uvažovaná podpostupnosť je prázdna, vložíme nový prvok na jej začiatok a úlohu sme vyriešili.

2. Ak uvažovaná podpostupnosť nie je prázdna, pozrime sa do jej stredu. Porovnajme hodnotu prvku v strede  s tým, ktorý chceme vložiť.   

• Ak je vkladaný prvok rovný tomu v strede, môžeme ho vložiť pred stredný prvok. Pozíciu sme našli.

• Ak je vkladaný prvok väčší ako ten v strede, uvažujme ďalej len s pravou časťou podpostupnosti a pokračujeme bodom 1.

• Ak je vkladaný prvok menší ako ten v strede, uvažujme ďalej len s ľavou časťou podpostupnosti a pokračujeme bodom 1.

Výsledkom je, že nájdeme pozíciu kam je potrebné vložiť nový prvok. Podpostupnosti teda nemusíme vždy nanovo usporadúvať. Toto riešenie môže vyzerať nasledovne:

# Python
def median(podpostupnost):
    dlzka = len(podpostupnost)
    if dlzka % 2 == 0:
        return (podpostupnost[dlzka // 2 - 1] + podpostupnost[dlzka // 2]) / 2
    return podpostupnost[dlzka // 2]


def najdi_poziciu(hodnota, podpostupnost):
    lavy = 0
    pravy = len(podpostupnost) - 1
    while lavy <= pravy:
        stred = (lavy + pravy) // 2
        if podpostupnost[stred] == hodnota:
            return stred
        if hodnota < podpostupnost[stred]:
            pravy = stred - 1
        else:
            lavy = stred + 1
    return lavy


def klzavy_median_2(postupnost, dlzka):
    mediany = []
    podpostupnost = postupnost[:dlzka]
    podpostupnost.sort()
    mediany.append(median(podpostupnost))
    for index in range(len(postupnost) - dlzka):
        podpostupnost.remove(postupnost[index])
        pridavany_prvok = postupnost[index + dlzka]
        pozicia_pridavaneho = najdi_poziciu(pridavany_prvok, podpostupnost)
        podpostupnost.insert(pozicia_pridavaneho, pridavany_prvok)
        mediany.append(median(podpostupnost))
    return mediany

Naše riešenie sme vylepšili, pretože nemusíme nové podpostupnosti vždy usporadúvať. Skúsme ho vylepšiť ešte viac.

Všimnime si, že keď z podpostupnosti odstraňujeme prvý pridaný prvok, použijeme príkaz zoznamu remove(). Aby Python našiel v podpostupnosti prvok, ktorý chceme odstrániť, musí celú podpostupnosť prehľadať (presnejšie, kým prvok nenájde). Pozíciu prvku, ktorú má Python z podpostupnosti odstrániť vieme nájsť aj šikovnejšie. Využijeme fakt, že podpostupnosť je usporiadaná a pre hľadanie pozícii už máme vytvorenú funkciu najdi_poziciu().

Riešenie s týmto vylepšením môže vyzerať nasledovne:

# Python
def median(podpostupnost):
    dlzka = len(podpostupnost)
    if dlzka % 2 == 0:
        return (podpostupnost[dlzka // 2 - 1] + podpostupnost[dlzka // 2]) / 2
    return podpostupnost[dlzka // 2]


def najdi_poziciu(hodnota, podpostupnost):
    lavy = 0
    pravy = len(podpostupnost) - 1
    while lavy <= pravy:
        stred = (lavy + pravy) // 2
        if podpostupnost[stred] == hodnota:
            return stred
        if hodnota < podpostupnost[stred]:
            pravy = stred - 1
        else:
            lavy = stred + 1
    return lavy


def klzavy_median_3(postupnost, dlzka):
    mediany = []
    podpostupnost = postupnost[:dlzka]
    podpostupnost.sort()
    mediany.append(median(podpostupnost))
    for index in range(len(postupnost) - dlzka):
        pozicia_odstranovaneho = najdi_poziciu(postupnost[index], podpostupnost)
        podpostupnost.pop(pozicia_odstranovaneho)
        pridavany_prvok = postupnost[index + dlzka]
        pozicia_pridavaneho = najdi_poziciu(pridavany_prvok, podpostupnost)
        podpostupnost.insert(pozicia_pridavaneho, pridavany_prvok)
        mediany.append(median(podpostupnost))
    return mediany

Pozrime sa ešte na to, ako "úspešné" sú naše vylepšenia. Namiesto teoretickej analýzy otestujme rýchlosť našich funkcií. Testov by sme mali realizovať niekoľko, aby záver bol čo najmenej ovplyvnený nejakou náhodou, ktorá sa vyskytla práve v čase testovania niektorej z funkcií. Zároveň uvažujme veľké množstvá dát, lebo pri malých množstvách nemusí byť úspora tak dobre viditeľná.

Len pre ilustráciu. Otestovali sme rýchlosť našich funkcií niekoľko krát pre rôzne dlhé postupnosti a rôzne dlhé podpostupnosti. Každú funkciu sme spustili 30x a v tabuľke uvádzame priemerný čas jej behu:

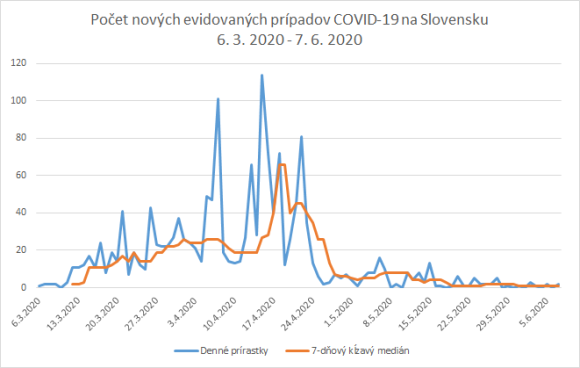
Pri malých dĺžkach podpostupností sú uvedené funkcie +- rovnako rýchlo. Rozdiel sa začne prejavovať pri väčších dĺžkach podpostupností. Zoberme si toto poučenie aj do budúcnosti. Ak navrhujeme nejaké riešenie, uvažujme o "veľkých" vstupoch. Až tam sa začne prejavovať efektivita našich algoritmov.

Na záver uvádzame jedno praktické využitie kĺzavého mediánu. Nasledujúci graf zobrazuje nové evidované prípady ochorenia na COVID-19 na Slovensku a 7-dňový kĺzavý medián. Z obrázku je viditeľné, že kĺzavý medián nie je ovplyvnený lokálnymi extrémnymi hodnotami, takže je z neho lepšie viditeľný trend vývoja počtu ochorení.

A ešte jedno malé, možno pre niekoho prekvapivé zamyslenie. Pri končiacich opatreniach v súvislosti s COVID-19 na Slovensku sme často počuli, že 7-dňový kĺzavý medián pre nové potvrdené prípady ochorenia má hodnotu 0. Aký môže byť v skutočnosti počet nových prípadov?

Aký je 7-dňový kĺzavý medián pre postupnosť hodnôt?

[1000, 0, 1000, 0, 1000, 0, 0, 1000, 0, 1000, 0, 1000, 0, 0, 1000, 0, 1000, 0, 1000, 0, 0, 1000]

Vaše zaujímavé riešenia a najčastejšie chyby

Všetky tímy, ktoré túto úlohu riešili odovzdali správne riešenie. Rozdiel bol len v efektívnosti jednotlivých riešení. Väčšina riešení sa spoľahla na vstavané funkcie a metódy zoznamov, podobne ako vyššie uvedené riešenie klzavy_median_1(). Našli sa však aj dva tímy (HairyElephants, seesharp) ktoré využili binárne vyhľadávanie (viď funkcia najdi_poziciu()) a zvýšili tak efektívnosť riešenia.

Na jednej strane je pre programátora výhodné využívať funkcionalitu, ktorú mu daný programovací jazyk poskytuje. Na druhej strane si treba uvedomiť, či pre uvedené potreby nevieme nájsť efektívnejšie riešenie. Namiesto sústavného usporadúvania (zoznam.sort()) udržujme zoznam usporiadaný. Namiesto mazania prvku (zoznam.remove()) využime fakt, že zoznam je usporiadaný a nájdime pozíciu mazaného prvku priamo.