PALMA junior
Úloha o automatickom vyhodnocovaní sudoku

Autorské riešenie
[stiahni py]                                       

• Počet riešiteľov: 4 / 4 = 100 %

• Úspešnosť riešenia: 6.5 / 9 = 72 %

V riešení tejto úlohy musíme navrhnúť nástroj, pomocou ktorého sa dajú kontrolovať vyplnené mriežky čísiel, či sú riešeniami sudoku. Úlohu máme trochu zjednodušenú, lebo podľa zadania môžeme predpokladať, že mriežka má korektný rozmer a v každom okienku je zadané číslo.

Pozrime sa, ako takáto mriežka vyzerá a čo by mala obsahovať. Príklady sudoku rôznych úrovní sú uvedené v nasledujúcej tabuľke. Všimnime si, že v poslednom riadku sme vyjadrili vlastnosti sudoku všeobecne.

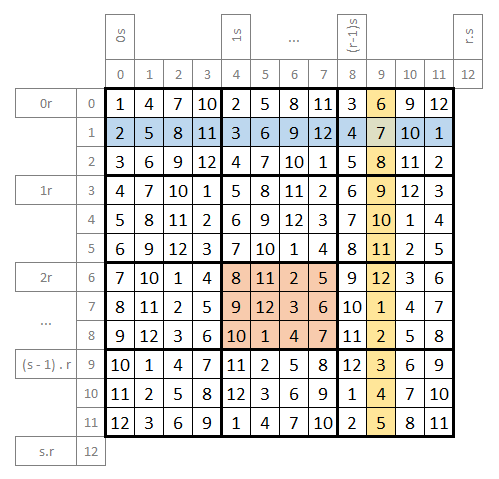
Zo samotnej mriežky nedokážeme určiť, akej úrovne sudoku je. Preto jedným z parametrov výslednej funkcie musí byť aj úroveň sudoku. Úroveň sudoku je určená dvoma prirodzenými číslami, ktoré predstavujú rozmer malej obdĺžnikovej oblasti (počet riadkov a počet stĺpcov). V ukážke nižšie je sudoku úrovne 3 x 4.

Pozrime sa, čo v danej mriežke musíme kontrolovať.

Každý  stĺpec , každý  riadok  a každý z vyznačených   obdĺžnikov  by mal obsahovať všetky požadované čísla (v ukážke vyššie sú to čísla 1 .. 12). Žiadne nesmie byť navyše a žiadne nesmie chýbať.

Ak sa pozrieme na riadky, stĺpce a malé obdĺžniky zistíme, že majú niečo spoločné. Všetko sú to nejaké obdĺžnikové oblasti v mriežke. Každú z nich vieme definovať pomocou intervalu čísiel riadkov a intervalu čísiel stĺpcov, ktorých hodnoty obsahuje. Pre lepšiu predstavu sme v obrázku vyššie významné čísla riadkov a stĺpcov vyznačili šedým písmom.

V predchádzajúcom obrázku

• vyznačený  modrý  riadok  definujeme nasledovne: [1, 2) × [0, 12),

• vyznačený  žltý  stĺpec  definujeme nasledovne: [0, 12) × [9, 10),

• vyznačenú  obdĺžnikovú oblasť  definujeme nasledovne: [6, 9) × [4, 8)

Hranatá zátvorka znamená, že hodnota do intervalu patrí (uzatvorený interval). Okrúhla zátvorka znamená, že hodnota do intervalu nepatrí (otvorený interval).

Určime si intervaly riadkov, stĺpcov a oblastí pre konkrétnu tabuľku a potom sa pokúsme tieto intervaly zovšeobecniť. Konkrétne hodnoty nám poslúžia aj ako kontrola, či sme pri zovšeobecnení nespravili chybu.

Riadky, stĺpce a malé obdĺžniky vieme kontrolovať pomocou rovnakej funkcie. Nazvime si ju napr. je_oblast_ok(). Stačí, ak jej pošleme, akú oblasť v akej mriežke má skontrolovať a aká je úroveň kontrolovaného sudoku. Výsledný program môže vyzerať nasledovne:

# Python
def je_oblast_ok(r1, r2, s1, s2, mriezka, r, s):
    cisla = list(range(1, r * s + 1))
    for riadok in range(r1, r2):
        for stlpec in range(s1, s2):
            if mriezka[riadok][stlpec] in cisla:
                cisla.remove(mriezka[riadok][stlpec])
            else:
                return False
    return True

def je_riesenie_sudoku(mriezka, r, s):
    #kontrola riadkov
    for riadok in range(s * r):
        if not je_oblast_ok(riadok, riadok + 1, 0, r * s, mriezka, r, s):
            return False
    #kontrola stlpcov
    for stlpec in range(r * s):
        if not je_oblast_ok(0, s * r, stlpec, stlpec + 1, mriezka, r, s):
            return False
    #kontrola oblasti
    for riadok in range(0, s * r, r):
        for stlpec in range (0, r * s, s):
            if not je_oblast_ok(riadok, riadok + r, stlpec, stlpec + s, mriezka, r, s):
                return False
    return True

Pozrime sa najskôr na funkciu je_oblast_ok(). V parametroch jej pošleme:

• krajné hodnoty intervalov čísiel riadkov a čísiel stĺpcov oblasti, ktorú ma skontrolovať,

• samotnú mriežku,

• úroveň sudoku - počet riadkov a počet stĺpcov malého obdĺžnika.

Najskôr si vytvoríme zoznam čísiel cisla, ktoré v oblasti musia byť umiestnené. Postupne prechádzame číslami oblasti (cez všetky riadky a stĺpce) a každé nájdené číslo z nášho zoznamu odstránime. Ak číslo v zozname nie je, znamená to, že sme ho už odstránili alebo také číslo by tam ani nemalo byť. Vieme teda, že oblasť je chybná. Ak k takejto situácii nedôjde, oblasť je vyplnená správne.

Funkcia je_riesenie_sudoku() dostane ako parameter:

• samotnú vyplnenú mriežku,

• úroveň sudoku - počet riadkov a počet stĺpcov malého obdĺžnika.

Potom postupne kontrolujeme riadky, stĺpce a malé obdĺžniky mriežky. Každú z týchto oblastí posielame na kontrolu. Ak niektorá z nich neprejde kontrolou, ďalej kontrolovať nemusíme a vieme, že vyplnená mriežka nie je riešením sudoku. Ak všetky kontrolované oblasti prešli kontrolou, vyplnená mriežka je riešením sudoku.

Dobrá rada na záver: Výsledný program nie je nejako zvlášť rozsiahly. Obsahuje však množstvo indexov pri ktorých je jednoduché sa pomýliť. Aby sme tomu zabránili, spravili sme si podrobnú analýzu ešte pred samotným programovaním. V tabuľke sme uviedli čísla riadkov a stĺpcov pre konkrétne oblasti konkrétnej mriežky. Potom sme čísla riadkov a čísla stĺpcov oblasti zapísali všeobecne pre ľubovoľnú mriežku. Pre kontrolu správnosti nám poslúžili konkrétne hodnoty. Samotný program je už len "prepisom" všeobecných vzťahov z tabuľky.

Vaše zaujímavé riešenia a najčastejšie chyby

Očakávali sme, že problémy vám spôsobí množstvo indexov a ich zmien s ktorými je potrebné pracovať. Ukázalo sa, že s týmto ste si poradili veľmi dobre. Najčastejšou chybou bolo zlé vyhodnocovanie jednotlivých oblastí. Niektorí predpokladali, že v danej oblasti budú len očakávané čísla, prípadne sa niektoré z nich budú opakovať. V mriežke však môžu byť ľubovoľné čísla (napr. -5).

Zaujímavé riešenie poslal tím Bubák v.7 Amavet 971. Úroveň sudoku určil len jedným číslom. Potom analyzoval mriežku a snažil sa zistiť, pre akú úroveň (r x s) sú oblasti vyplnené. Toto riešenie je problematické v tom, že ak niekto sudoku úrovne r x s vyrieši ako sudoku úrovne s x r, zrejme jeho riešenie nebude správne. Program ho však uzná za správne.