PALMA junior
Úloha o viaccípych prepletaných hviezdach

Autorské riešenie
[stiahni [py]]

• Počet riešiteľov:  4 / 4 = 100.0 %

• Úspešnosť riešenia:  4.75 / 7 = 67.9 %

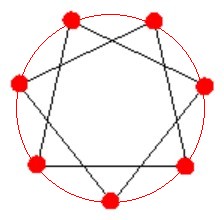
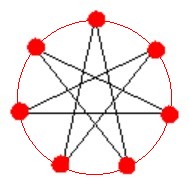
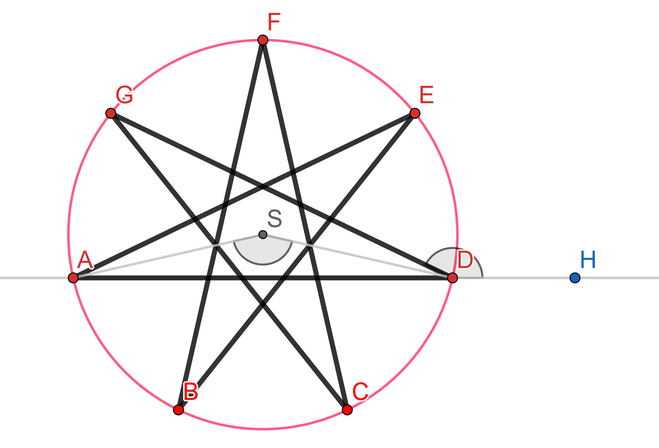
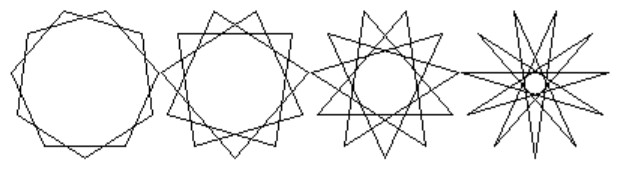
Pri hľadaní všetkých riešení sa najprv pozrime na obrázky so zadania. Doplnením pomocných prvkov - opísanej kružnice a zvýraznením vrcholov (označených červenou farbou) môžme premyslieť ako vznikli uvedené riešenia.

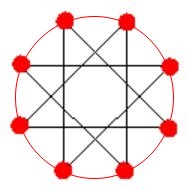
Hviezda v ľavo vznikla spájaním každého druhého bodu na pomocnej kružnici a hviezda vpravo spájaním každého tretieho bodu na pomocnej kružnici.

Keď sa lepšie pozrieme na obrázky, môžeme tiež povedať, že hviezda vľavo vznika spájaním každého piateho bodu a hviezda vpravo spájaním každého štvrtého bodu

Pozrime sa na ostatné prípady. Spájaním každého nasledujúceho (prvého) bodu resp. každého šiesteho bodu by sme dostali len pravidelný sedemuholník. Takže sedemcípu hviezdu vieme nakresliť 2 spôsobmi, a to s krokom 2 a krokom 3.

Ešte sa pozrime na osemcípu hviezdu. Pri nej pripadajú možné kroky z množniny {2, 3, 4, 5, 6}. Keďže kroky 5 a 6 dávajú rovnaké výsledky ako kroky 8-5=3 a 8-6=2, stačí nám uvažovať kroky len z množiny {2, 3, 4}. Pri krokoch 2 a 4, nevieme vykresliť celú osemcípu hviezdu, lebo čísla 2 a 4 sú delitele čísla 8.

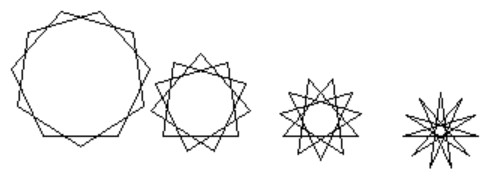
Vo všeobecnosti pre zadané prirodzené číslo N budeme vedieť nájsť všetky N-cípe hviezdy tak, že ich hodnoty kroku budú z množiny všetkých nesúdeliteľných  čísel s číslom N väčšie ako 2 a menšie ako hodnota N/2. Napríklad pre N=11, zistíme, že hodnoty kroku sú z množiny {2, 3, 4, 5}.

Pre výpočet zoznamu nesúdeliteľov čísla N použijeme funkciu zoznam_nesudelitelnych(n) a k nej pomocnú funkciu nsd(a,b) na výpočet najväčšieho spoločného deliteľa. Programový kód týchto funkcií môže vyzerať nasledovne:

def nsd(a, b):
    ''' Vypočíta najväčší spoločný deliteľ dvoch prirodzených čísel'''
    while a != b:
        if a > b:
            a = a - b
        else:
            b = b - a
    return a


def zoznam_nesudelitelnych(n):
    ''' Vráti zoznam nesúdeliteľmých čísel so zadaným číslom'''
    return [cislo for cislo in range(2, n // 2 + 1) if nsd(cislo, n) == 1]

Ak vieme pre zadané číslo N zistiť množinu jeho nesúdeliteľov, z ktorej budeme vyberať hodnotu kroku K, potom ešte potrebujeme navrhnúť postup ako vykresliť N-cípu hviezdu s krokom K.

Na základe obrázku s vyznačenými bodmi a uhlami, určíme uhol natočenia "korytnačky" po vykreslení každého ramena N-cípej hviezdy. Po nakreslení úsečky AD sa potrebuje "korytnačka" otočiť o  ∠HDG, aby potom nakreslila nadväzujúcu úsečku DG.

Dá sa ľahko ukázať, že veľkosť ∠HDG je rovná veľkosti ∠ASD (súčet veľkostí  ∠SAD a ∠SDA je rovný veľkosti ∠ADG). Veľkosť  ∠ASD je rovná výrazu (360 / N) * K.

Výsledné riešenie celej úlohy zapísané v jazyku Python môže vyzerať nasledovne:

import turtle


def nsd(a, b):
    ''' Vypočíta najväčší spoločný deliteľ dvoch prirodzených čísel'''
    while a != b:
        if a > b:
            a = a - b
        else:
            b = b - a
    return a


def zoznam_nesudelitelnych(n):
    ''' Vráti zoznam nesúdeliteľmých čísel so zadaným číslom'''
    return [cislo for cislo in range(2, n // 2 + 1) if nsd(cislo, n) == 1]


def vykresli_hviezdu(pocet_cipov, krok):
    ''' Vykreslí n-cípu hviezdu s krokom k'''
    for i in range(pocet_cipov):
        pero.forward(50)
        pero.left(360 * krok / pocet_cipov)


def vykresli_hviezdy(pocet_cipov):
    ''' Vykreslí v rade všetky možné n-cípe hviezdy'''
    for krok in zoznam_nesudelitelnych(pocet_cipov):
        vykresli_hviezdu(pocet_cipov, krok)
        pero.penup()
        pero.forward(80)
        pero.pendown()


tabula = turtle.Screen()
pero = turtle.Turtle()
tabula.delay(0)

vykresli_hviezdy(11)

tabula.mainloop()

Veľmi krátke riešenie pre vykreslenie N-cípej hviezdy s krokom K ponúka samotná metóda circle():

def vykresli_hviezdu2(pocet_cipov, krok):
    ''' vykreslí hviezdu so zadaným počtom cípov a krokom'''
    pero.circle(50, krok * 360, pocet_cipov)

Pomocou nej by sme vykreslili hviezdy, ktorých vrcholy by boli totožné a ležali by na tej istej kružnici, ale jednotlivé hviezdy by mali rôzne dľžky ramien, čo je uvedené ako podmienka v zadaní úlohy.

Táto súťažná úloha je zameraná na dôslednú analýzu matematického problému, využitie deliteľnosti čísel pri  nájdení všetkých riešení úlohy, na použitie stratégií riešenia problémov - hľadanie vzoru a pomocný prvok, na prácu s dátovou štruktúrou zoznam, precvičenie príkazov korytnačej grafiky a príkazov opakovania a vetvenia a funkcii s parametrami a výstupmi.

Vaše zaujímavé riešenia a najčastejšie chyby

Do riešenia tejto úlohy sa zapojili 4 tímy z kategórie GURU. Plný počet bodov získal len jeden tím Šedá eminencia dodekahedrónov, k čomu im gratulujeme.

V riešeniach sme zaregistrovali nasledovné chyby, vychádzajúce z nedôslednej analýzy problému:

• vykreslenie len N-cípych hviezd s nepárnym N a s krokom 2,
• vykreslenie navyše hviezd, ktoré sa nedajú nakresliť jedným ťahom (napr. 6-cípej),
• nesprávne určená hranica pre krok K v hlavnom cykle (s).