PALMA junior
Úloha o bludisku

Autorské riešenie
[stiahni imp : py]

• Počet riešiteľov: 7 / 8 = 88 %

• Úspešnosť riešenia: 4,36 / 7 = 62 %

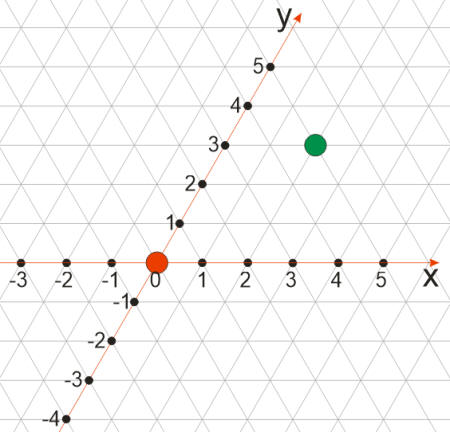
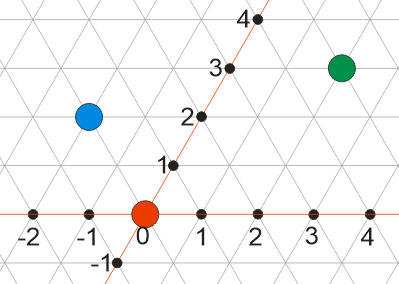
Na trojuholníkovú mriežku sa môžeme pozrieť ako na súradnicový systém. Každému bodu mriežky môžeme priradiť nejakú súradnicu.

Na obrázku sú zvýraznené nami zvolené súradnicové osi x a y. Štartovacej miestnosti priradíme súradnice [0, 0], miestnosť s východom bude mať súradnice [2, 3].

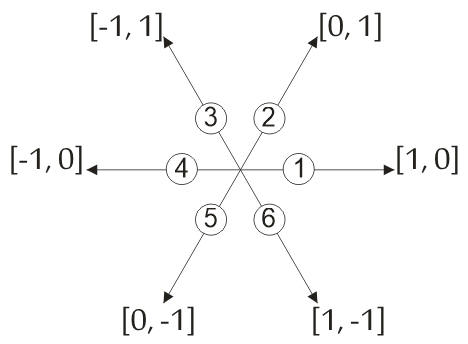
 Stred súradnicovej sústavy nemusí byť v štartovacej miestnosti. Táto voľba nám však zjednoduší riešenie. Podobne aj pre osi x a y sme si mohli zvoliť ľubovoľnú dvojicu smerov.

Najprv zistíme súradnice hráča (súradnice miestnosti, v ktorej stlačil bezpečnostné tlačidlo). Využijeme to, že hráč začal svoj pohyb v bludisku na pozícii [0, 0] a tieto súradnice budeme postupne meniť na základe postupnosti smerov uložených v premennej zaznam_pohybu. Tento prepočet realizujeme v procedúre/funkcii suradnice_hraca jednoduchým testovaním, pričom využívame kódy možných smerov pohybu. Pre každý smer vieme povedať, ako sa zmenia súradnice hráča.

Získané súradnice aktuálnej polohy hráča (miestnosť, v ktorej hráč stlačil bezpečnostné tlačidlo) použijeme na vytvorenie zoznamu smerov, ktorými sa hráč dostane do miestnosti s východom.

Zoznam s kódmi smerov, pomocou ktorého sa hráč dostane najkratšou cestou do miestnosti s východom, vráti procedúra/funkcia vychod. Samozrejme, nie je to vždy jediná možná najkratšia cesta - poradie smerov sa môže líšiť podľa postupnosti zápisu jednotlivých podmienok. Teda, ak uvažujeme o situácii na obrázku zo zadania úlohy, možnými výsledkami sú zoznamy [1, 1, 1, 1, 2], [2, 1, 1, 1, 1]...

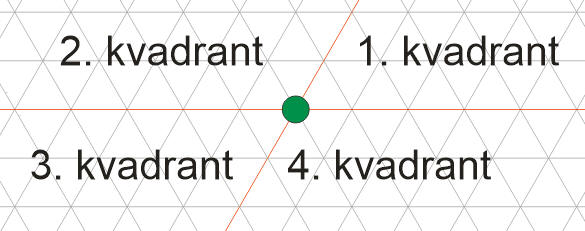
Pri riešení úlohy budeme hľadať zoznam pohybov hráča do miestnosti s východom. Poznáme súradnice miestnosti, kde hráč stlačil tlačidlo a súradnice miestnosti s východom. Hľadáme teda takú najkratšiu postupnosť smerov, aby sa súradnice hráča zmenili na súradnice miestnosti s východom.

Súradnicovú sústavu (trojuholníkovú sieť) pomyselne rozdelíme (vzhľadom na pozíciu miestnosti s východom) na štyri oblasti (tzv. kvadranty) a podľa toho, v ktorej z týchto štyroch častí sa hráč v simulácii nachádza, vytvoríme zoznam smerov, ktorý dovedie hráča do miestnosti s východom.

Z rozdielu súradníc miestnosti s východom a súradníc hráča, vieme zistiť v ktorom kvadrante sa hráč nachádza a ktoré zo smerov môžeme použiť na prechod do miestnosti s východom. V niektorých kvadrantoch vieme dvojicu smerov nahradiť - zložiť do jedného smeru.

Ak sa hráč nachádza v kvadrantoch 1. alebo 3. cesta k východu je jednoduchá. Použijeme len dva zo smerov. Použitie každého z nich zmení hráčovi buď x-ovú alebo y-ovú súradnicu.

Ak sa hráč nachádza v kvadrantoch 2. alebo 4. riešenie bude trochu náročnejšie. Tu by sme mali prednosti používať smery, ktoré menia aj x-ovú aj y-ovú súradnicu hráča súčasne. Namiesto dvoch krokov môžeme teda spraviť len jeden. Chceme totiž minimalizovať počet krokov k východu.

Riešenie úlohy môže vyzerať nasledovne:

def suradnice_hraca(zaznam_pohybu):
    x, y = 0, 0
    for smer in zaznam_pohybu:
        if smer == 1:
            x += 1
        elif smer == 2:
            y += 1
        elif smer == 3:
            x -= 1
            y += 1
        elif smer == 4:
            x -= 1
        elif smer == 5:
            y -= 1
        elif smer == 6:
            x += 1
            y -= 1
    return [x, y]


def vychod(zaznam_pohybu):
    x_vychod, y_vychod = 2, 3
    suradnice = suradnice_hraca(zaznam_pohybu)
    x_hraca = suradnice[0]
    y_hraca = suradnice[1]
    zmena_x = x_vychod - x_hraca
    zmena_y = y_vychod - y_hraca
    if zmena_y >= 0:
        if zmena_x >= 0:
            navrat = [1] * abs(zmena_x)
            navrat = navrat + [2] * abs(zmena_y)
        else:
            pocet_dvojkrokov = min(abs(zmena_x), abs(zmena_y))
            navrat = [4] * (abs(zmena_x) - pocet_dvojkrokov)
            navrat = navrat + [2] * (abs(zmena_y) - pocet_dvojkrokov)
            navrat = navrat + [3] * pocet_dvojkrokov
    else:
        if zmena_x >= 0:
            pocet_dvojkrokov = min(abs(zmena_x), abs(zmena_y))
            navrat = [1] * (abs(zmena_x) - pocet_dvojkrokov)
            navrat = navrat + [5] * (abs(zmena_y) - pocet_dvojkrokov)
            navrat = navrat + [6] * pocet_dvojkrokov
        else:
            navrat = [5] * abs(zmena_y)
            navrat = navrat + [4] * abs(zmena_x)
    return navrat


zaznam_pohybu = [2, 2, 1, 5, 4, 4, 5, 3]
print(vychod(zaznam_pohybu))

Vaše zaujímavé riešenia a najčastejšie chyby

Úlohu riešilo 7 tímov, 2 tímy z kategórie expert a 5 tímov z kategórie guru. Jeden tím úlohu vyriešil len pre jeden špeciálny prípad. Ostatné tímy sa s touto úlohou dobre popasovali.

Najčastejšie boli chyby len v tom, že žiaci neošetrili všetky podmienky a niektorí neošetrili ani to, či sa v zozname nachádzajú naozaj len hodnoty 1-6. Zaujímavé, avšak nie optimálne, bolo riešenie, v ktorom bolo pre hráčov odporúčané vrátiť sa na štart a zo štartu prejsť najkratšou cestou do cieľa.  Niektoré tímy na riešenie používali "klasickú" súradnicovú sústavu, v ktorej okrem celých čísel používali na  určenie miestnosti vo vrchole trojuholníka aj desatinné čísla - konkrétne polovice. V tomto prípade sa stalo, že žiaci neošetrili riešenie, kedy x-ová súradnica je síce správna, ale neexistuje krok smerom "priamo nahor", ktorý by bol optimálny, a teda riešenie sa zacyklilo.