PALMA junior
Úloha o programovaní plničky sieťok na jablká

Autorské riešenie
[stiahni py]                                       

• Počet riešiteľov: 5 / 15 = 33 %

• Úspešnosť riešenia: 2.8 / 8 = 35 %

V  riešení tejto úlohy sa očakáva, že navrhneme nejakú dobrú stratégiu pre umiestňovanie jabĺk do sieťok. Pripomeňme si podmienky, ktoré v riešení musíme dodržať:

• Plnička by mala jablká triediť dovtedy, kým nie je zásobník prázdny.

• Ak vyberieme nejaké jablko zo zásobníka, musíme rozhodnúť kam ho dáme. Máme len dve možnosti:

  • ak jablko vyhovuje obchodníkom, musíme ho dať do niektorej zo sieťok,

  • ak jablko nevyhovuje obchodníkom, musíme ho dať do odpadu.

• Ak sme jablko vložili do sieťky, už ho odtiaľ nevieme vybrať (vieme len vysypať obsah celej sieťky späť do zásobníka).

Pozrime sa bližšie na to, čo to znamená: "musíme ho dať do niektorej zo sieťok":

• Ak jablko umiestňujeme do sieťky, musíme rozhodnúť do ktorej. Máme dve možnosti:

  1. Zvolíme nejakú sieťku a po vložení jablka overíme, či sieťka vyhovuje požiadavkám obchodníkov.

     • Ak je hmotnosť sieťky príliš vysoká, vysypeme jej obsah späť do zásobníka.

     • Ak hmotnosť sieťky spĺňa požiadavky obchodníkov, presunieme ju do skladu.

     • Ak je hmotnosť sieťka príliš nízka, ponecháme ju na mieste. 

  2. Zvolíme nejakú sieťku tak, aby po vložení jablka do sieťky hmotnosť jabĺk v sieťke nepresiahla limit obchodníkov.

     • V tomto prípade musíme vymyslieť čo urobiť v situácii, ak žiadna taká sieťka nie je. Inak sa plnička zablokuje. Zrejme budeme musieť obsah niektorej zo sieťok vysypať späť do zásobníka.

Základná šablóna pre prvý prístup môže vyzerať nasledovne: 

# Python
def spusti_plnicku():
    # vyberieme nejakú sieťku a vložíme jablko tam
    # otestujeme novú hmotnosť sieťky
    plnicka = Plnicka()
    plnicka.napln_zasobnik()

    while not plnicka.je_prazdny_zasobnik:
        plnicka.vyber_jablko_zo_zasobnika()
        if not je_jablko_dobre(plnicka.jablko):
            plnicka.jablko_do_odpadu()
            continue

        #----------- vyber naj sietku -----------

        cislo_naj_sietky = #podľa kritérií vyberieme najlepšiu sieťku

        #----------- vyber naj sietku -----------

        plnicka.jablko_do_sietky(cislo_naj_sietky)
        if plnicka.hmotnost_sietky(cislo_naj_sietky) > 1000 * 1.05:
            plnicka.sietka_do_zasobnika(cislo_naj_sietky)
        elif plnicka.hmotnost_sietky(cislo_naj_sietky) >= 1000 * 0.95:
            plnicka.sietka_do_skladu(cislo_naj_sietky)

Základná šablóna pre druhý prístup môže vyzerať nasledovne:  

#Python
def spusti_plnicku():
    # otestujeme hmotnosti sieťok a potom jablko vložíme 
    # do vybranej sieťky + otestujeme novú hmotnosť sieťky
    plnicka = Plnicka()
    plnicka.napln_zasobnik()

    while not plnicka.je_prazdny_zasobnik:
        plnicka.vyber_jablko_zo_zasobnika()
        if not je_jablko_dobre(plnicka.jablko):
            plnicka.jablko_do_odpadu()
            continue

        #----------- vyber naj sietku -----------
        
        cislo_naj_sietky = #vyberieme najlepšiu vhodnú sieťku,
                           #kam sa jablko ešte vojde
                           #ak sa jablko nikam nevojde
                           #vyber sieťku a vysyp ju späť do zásobníka

        #----------- vyber naj sietku -----------

        plnicka.jablko_do_sietky(cislo_naj_sietky)
        if plnicka.hmotnost_sietky(cislo_naj_sietky) >= 1000 * 0.95:
            plnicka.sietka_do_skladu(cislo_naj_sietky)

Ak sa pozrieme na uvedené šablóny, tak pre minimalizáciu počtu jabĺk vrátených do zásobníka bude rozhodujúce zrejme to, podľa akého kritéria vyberieme "cislo_naj_sietky". Pozrime sa na niektoré z nich:

• z možných sieťok náhodne niektorú vyberieme,

• vyberme tú, ktorá má najmenšiu hmotnosť,

• vyberme tú, ktorá má najväčšiu hmotnosť, 

• vyberieme prvú sieťku, ktorá vyhovuje,

• nejaká kombinácia predchádzajúcich,

• nejaké iné kritérium.

Pokúsme sa ich vzájomne porovnať. Tu je dôležité, aby sme ich testovali na rovnakej postupnosti jabĺk a aby počet jabĺk bol dostatočný. Ak by sme zvolili príliš malý počet, riskujeme že takáto konkrétna postupnosť bude taká špecifická, že "zvýhodní" niektorú zo stratégií.

Naprogramovali sme uvedené stratégie a spustili sme ich niekoľko krát na postupnosti 100000 náhodne vygenerovaných jabĺk (požili sme rovnaký generátor aký používa metóda napln_zasobnik()). Výsledky sú v nasledujúcej tabuľke: 

Prvý prístup: Vyberieme nejakú sieťku a vložíme jablko tam. Sieťku otestujeme. 

Druhý prístup: Vyber sieťky, do ktorých sa jablko ešte vojde. 

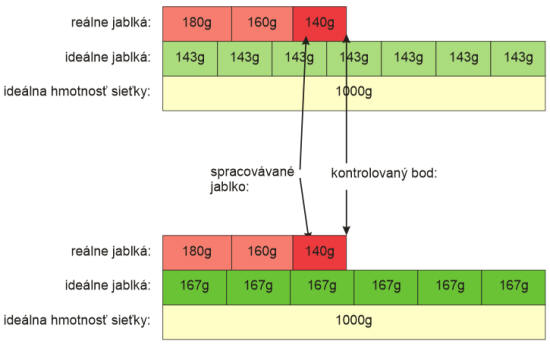
 * - občas sa stalo, že plnička sa zacyklila (počet vrátených jabĺk bol príliš veľký)

** - prakticky vždy sa plnička zacyklila (počet vrátených jabĺk bol príliš veľký)

Vidíme, že tieto naivné stratégie nefungujú alebo fungujú veľmi zle. Možno by jablká nakoniec aj utriedili do sieťok, ale boli by také doudierané, že by boli prakticky nepredajné.

Prvý prístup je podľa očakávania horší. Jablko niekedy (v skutočnosti dosť často) vkladáme aj do takej sieťky, kam sa určite nevojde. V druhom prípade vyberáme len také sieťky, kam sa jablko ešte vojde. Ale ani druhý prístup nie je žiadna sláva. Jediná stratégia ktorá aspoň ako tak funguje je založená na náhode. Problémom je, sieťky neplníme nejako premyslene. Berieme len celkovú hmotnosť. Keď už je sieťka skoro plná je ťažké nájsť pre ňu vhodné jablko aby sa naplnila tak, aby sme ju mohli presunúť do skladu.

Poďme vymyslieť nejaký premyslenejší spôsob plnenia. Hmotnosť jablka, ktoré vkladáme do sieťky je 150g +- 20%. Zoberme si priemerné jablko. To bude vážiť približne 150g. Ak by sme do sieťky vkladali priemerné jablká, mohli by sme tam vložiť: 1000g / 150g = 6,67 jablka. Keďže musíme vložiť celý počet jabĺk, zaokrúhlime to na 7. V tomto prípade by bolo vhodné, keby priemerné jablko vážilo 1000g / 7 = 143g.

Pokúsme sa teda jablká do sieťok ukladať tak, aby sa ich celková hmotnosť čo najmenej líšila od nejakého násobku čísla 143. Sieťku teda budeme vyberať tak, aby sa po vložení jablka do nej, kontrolovaný bod (pozri obrázok) čo najviac priblížil k nejakému násobku čísla 143.

Otestujme túto stratégiu. Funkcia spusti_plnicku() môže vyzerať nasledovne:

# Python
def spusti_plnicku_1():
    #Vyberieme sieťky kam sa jablko ešte vojde. Z nich vyberieme tú, 
    #ktorej hmotnosť sa po vložení jablka najviac priblíži k násobku
    # čísla 143. Ak nie je sieťka do ktorej sa jablko vojde, 
    #vysyp do zásobníka najťažšiu.')
    plnicka = Plnicka()
    plnicka.napln_zasobnik()

    while not plnicka.je_prazdny_zasobnik:
        plnicka.vyber_jablko_zo_zasobnika()
        if not je_jablko_dobre(plnicka.jablko):
            plnicka.jablko_do_odpadu()
            continue

        #----------- vyber naj sietku -----------
        vhodne_sietky = []
        for sietka in range(plnicka.pocet_sietok):
            if plnicka.hmotnost_sietky(sietka) + plnicka.jablko <= 1000 * 1.05:
                vhodne_sietky.append(sietka)
        if len(vhodne_sietky) > 0:
            cislo_naj_sietky = vhodne_sietky[0]
            for sietka in vhodne_sietky:
                if rozdiel_od_nasobku(plnicka.hmotnost_sietky(sietka) + 
                                      plnicka.jablko, 143) < \
                   rozdiel_od_nasobku(plnicka.hmotnost_sietky(cislo_naj_sietky) + 
                                      plnicka.jablko, 143):
                    cislo_naj_sietky = sietka
        else:
            cislo_naj_sietky = 0
            for sietka in range(plnicka.pocet_sietok):
                if plnicka.hmotnost_sietky(sietka) > \
                   plnicka.hmotnost_sietky(cislo_naj_sietky):
                    cislo_naj_sietky = sietka
            plnicka.sietka_do_zasobnika(cislo_naj_sietky)
        #----------- vyber naj sietku -----------

        plnicka.jablko_do_sietky(cislo_naj_sietky)
        if plnicka.hmotnost_sietky(cislo_naj_sietky) >= 1000 * 0.95:
            plnicka.sietka_do_skladu(cislo_naj_sietky)

Keď sme túto stratégiu opakovane aplikovali na rovnaké množstvo testovacích dát ako predchádzajúce, do zásobníka sa vracalo 6000 - 7000 jabĺk (len ojedinele sa plnička zacyklila). To je výrazné vylepšenie oproti predchádzajúcim stratégiám. Stále je to však pomerne veľa. Pokúsme sa to ešte vylepšiť.

Na začiatku tejto úvahy sme sa rozhodli, že počet jabĺk zaokrúhlime na 7 a ideálna hmotnosť jablka by mala byť 143g (1000g / 7). Lenže, ak zoberieme ťažšie jablká (a tie naše sú v priemere ťažšie), vojde sa ich tam menej. Ak by sme uvažovali 6 jabĺk, hmotnosť ideálneho jablka by mala byť 167g (1000g / 6). Dovoľme teda sieťky plniť na násobky 143g alebo na násobky 167g. Jablko teda vložíme tam, kde sa najviac priblížime k jednému alebo druhému násobku.

Na obrázku sa porovnávajú dve situácie. V prvej optimalizujeme sieťku na násobky 143 a v druhej na násobky 167. Vidíme, že v druhom prípade sa priblížime k násobku ideálneho jablka viac ako v prvom. Samozrejme, vopred nevieme povedať ku ktorému násobku chceme sieťku "optimalizovať". Vždy budeme testovať každú sieťku na obidva násobky a vyberieme ten, kde sa priblížime k násobku viac. Zo všetkých sieťok nakoniec vyberieme tú, v ktorej sa k niektorému násobku vieme dostať najbližšie. Funkcia spusti_plnicku() s vylepšenou stratégiou môže vyzerať nasledovne:

# Python
def spusti_plnicku_2():
    #Vyberieme sieťky kam sa jablko ešte vojde. Z nich vyberieme tú, 
    #ktorej hmotnosť sa po vložení jablka najviac priblíži k násobku čísla 143 
    #alebo 167. Ak nie je sieťka do ktorej sa jablko vojde, vysyp do zásobníka najťažšiu.')
    plnicka = Plnicka()
    plnicka.napln_zasobnik()

    while not plnicka.je_prazdny_zasobnik:
        plnicka.vyber_jablko_zo_zasobnika()
        if not je_jablko_dobre(plnicka.jablko):
            plnicka.jablko_do_odpadu()
            continue

        #----------- vyber naj sietku -----------
        vhodne_sietky = []
        for sietka in range(plnicka.pocet_sietok):
            if plnicka.hmotnost_sietky(sietka) + plnicka.jablko <= 1000 * 1.05:
                vhodne_sietky.append(sietka)
        if len(vhodne_sietky) > 0:
            cislo_naj_sietky = vhodne_sietky[0]
            for sietka in vhodne_sietky:
                rozdiel_akt_sietka = min(
                    rozdiel_od_nasobku(plnicka.hmotnost_sietky(sietka) + plnicka.jablko, 143), 
                    rozdiel_od_nasobku(plnicka.hmotnost_sietky(sietka) + plnicka.jablko, 167))
                rozdiel_naj_sietka = min(
                    rozdiel_od_nasobku(plnicka.hmotnost_sietky(cislo_naj_sietky) + 
                                       plnicka.jablko, 143), 
                    rozdiel_od_nasobku(plnicka.hmotnost_sietky(cislo_naj_sietky) + 
                                       plnicka.jablko, 167))
                if  rozdiel_akt_sietka < rozdiel_naj_sietka:
                    cislo_naj_sietky = sietka
        else:
            cislo_naj_sietky = 0
            for sietka in range(plnicka.pocet_sietok):
                if plnicka.hmotnost_sietky(sietka) > plnicka.hmotnost_sietky(cislo_naj_sietky):
                    cislo_naj_sietky = sietka
            plnicka.sietka_do_zasobnika(cislo_naj_sietky)
        #----------- vyber naj sietku -----------

        plnicka.jablko_do_sietky(cislo_naj_sietky)
        if plnicka.hmotnost_sietky(cislo_naj_sietky) >= 1000 * 0.95:
            plnicka.sietka_do_skladu(cislo_naj_sietky)

Keď sme túto stratégiu opakovane aplikovali na rovnaké množstvo testovacích dát ako predchádzajúcu, do zásobníka sa vracalo 0 jabĺk. To je ideálne riešenie.

Objektívne ale musíme priznať, že to neznamená, že tomu tak bude vždy. Len sa nám nepodarilo nájsť takú postupnosť jabĺk, aby sa nejaké muselo vrátiť späť do zásobníka alebo aby sa plnička zacyklila.

V každom prípade je možné experimentovať ďalej a skúmať aj iné stratégie. Môžeme meniť aj požiadavky obchodníkov na hmotnosť jablka a hmotnosť sieťky. Môžeme experimentovať s počtom sieťok, ktoré dokáže plnička súčasne plniť a pod.

Pre úplnosť ešte uvádzame funkcie, ktoré testujú jablko a vracajú rozdiel od násobku.

# Python
def je_jablko_dobre(jablko):
    return 150 * 0.8 <= jablko <= 150 * 1.2

def rozdiel_od_nasobku(cislo, nasobok):
    return min(cislo % nasobok, abs(cislo % -nasobok))

Vaše zaujímavé riešenia a najčastejšie chyby

Vyzerá to tak, že táto úloha vás trochu potrápila. Jediný tím, ktorý úspešne implementoval nejakú stratégiu bol tím guru main.py. Ich stratégia bola veľmi podobná stratégii spusti_plnicku_2(). Namiesto násobku čísla 143 sa však snažili priblížiť k násobku čísla 150. Keďže 1000 nie je násobkom 150, dosť čast sa im stalo, že posledné jablko sa už do sieťky nevošlo.