PALMA junior, Programovanie, ALgoritmy, MAtematika, súťaž pre mladých programátorov v Imagine

	PALMA junior

Úloha o kreslení ozubených kolies

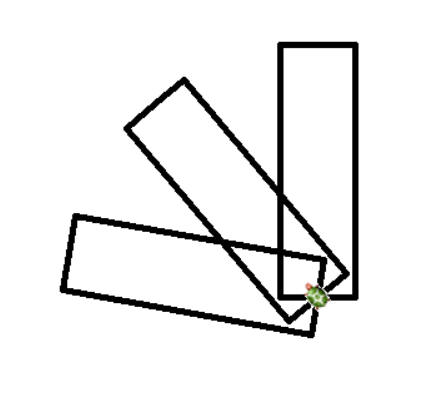
Autorské riešenie
[stiahni imp : py ]

Počet riešiteľov v : 11 / 17 = 65 %
Úspešnosť riešenia: 3,64 / 5 = 73 %

Úlohu je možné riešiť rôzne, uvedieme jednu z možností.

Zuby ozubeného kolesa navrhujeme nakresliť ako obdĺžníky, ktoré majú jeden spoločný bod v strede šírky každého obdľžníka. Všetky obdĺžníky začneme kresliť z toho istého bodu, a každý nasledujúci bude otočený o uhol 360/počet požadovaných zubov.

Na kreslenie obdĺžníka so šírkou :s a dĺžkou :d vytvoríme procedúru:

;Imagine logo
viem obdlznik :s :d
; parametre :s-sirka, :d-dlzka jedneho obdlznika

polygon [
nechFv "cierna
opakuj 2 [
do (:s/2)
vl 90
do :d
vl 90
do (:s/2)
]
]
koniec

Pri kreslení ozubeného kolesa postupujeme tak, že po nakreslení požadovaného počtu obdĺžníkov dookola nakreslíme kruh so stredom, kde sme začali kresliť aj obdĺžníky.

Keďže zuby a vzdialenosti medzi zubami majú byť rovnaké, aby zuby dobre zapadli, preto obvod vnútorného kruhu môžeme určiť takto: k = počet zubov x 2 x šírka zuba
Pre určenie obvodu kruhu platí vzťah: k = 2 x 3,14 x polomer
Z toho vieme určiť polomer kruhu, ktorý bude tvoriť vonkajší kruh kolesa:
polomer = (počet zubov x 2 x šírka zuba)/ 2 x 3,14

Dĺžka obdĺžníka pri kreslení ozubeného kolesa má byť väčšia ako polomer vnútorného kruhu práve o s/2, aby zuby susedných kolies dobre zapadli.

Ostane ešte nakresliť vnútorný a stredný kruh kolesa s daným polomerom.
Program v Imagine pre počet zubov :p a šírku jedného zuba :s môže vyzerať takto:

;Imagine logo
viem koliesko :p :s
; parametre :p-pocet zubov, :s-sirka jedneho zuba

; vypocet dlzky jedneho zuba
urobtu "polomer (:s * 2 * :p) / (2 * 3.141)

; kreslenie obdlznikov so zadanym poctom zubov
opakuj :p [
obdlznik :s :polomer+:s/2
vl 360/:p
]

; kreslenie vnutornych kruhov
bod 2*:polomer
nechFp "biela
bod :s
nechFp "cierna

koniec

Riešenie v Pythone:

Vo vzorovom riešení používame Pythonovskú korytnačiu grafiku s modulom turtle. Uprednostnili sme prístup import turtle pred prístupom from turtle import *, ktorý je síce stručnejší, ale je prehľadnejší pri práci s rôznymi objektami.
Podobne ako v Imagine, aj v Pythone úlohu si môžeme rozdeliť:
Vstupné parametre budú pocet - počet zubov ozubeného kolesa a s - šírka jedného zuba. Polomer určíme podobne, ako v Imagine: polomer = (s * 2 * :pocet) / (2 * 3.141)
Funkcia obdlznik (sirka, vyska) rieši kreslenie jedného obdľžníka.

Postup na kreslenie ozubeného kolieska je rovnaký, ako v Imagine. Riešenie v Pythone môže byť nasledovné:

#Úloha o kreslení ozubeného kolieska

					  
					  import
					  
					  turtle
					  
k = 
					  
					  turtle
					  
					  .
					  
					  Turtle
					  
					  (
					  
					  )
					  
p = 
					  
					  turtle
					  
					  .
					  
					  Screen
					  
					  (
					  
					  )
					  
pocet = 
					  
					  12
					  
s = 
					  
					  30
					  
#Výpočet polomeru, dľžky 
					  jedného zuba
polomer = 
					  
					  ( s
					  
					  *
					  
					  2
					  
					  *
					  
					  pocet
					  
					  )
					  
					  / 
					  
					  (
					  
					  2
					  
					  *
					  
					  3.141
					  
					  )
					  
#Kreslenie jedného 
					  obdĺžníka

					  def
					  
					  obdlznik
					  
					  (
					  
					  sirka, dlzka
					  
					  )
					  
					  :
    k. 
					  
					  right
					  
					  (
					  
					  90
					  
					  )
					  
    k.
					  
					  begin_fill
					  
					  (
					  
					  )
					  
					  for
					  
					  i 
					  
					  in
					  
					  range
					  
					  (
					  
					  2
					  
					  )
					  
					  :
        k.
					  
					  forward
					  
					  (
					  
					  sirka / 
					  
					  2
					  
					  )
					  
        k.
					  
					  left
					  
					  (
					  
					  90
					  
					  )
					  
        k.
					  
					  forward
					  
					  (
					  
					  dlzka
					  
					  )
					  
        k.
					  
					  left
					  
					  (
					  
					  90
					  
					  )
					  
        k.
					  
					  forward
					  
					  (
					  
					  sirka / 
					  
					  2
					  
					  )
					  
    k.
					  
					  end_fill
					  
					  (
					  
					  )
					  
    k.
					  
					  left
					  
					  (
					  
					  90
					  
					  )
					  
#Kreslenie obdĺžníkov 
					  so zadaným počtom zubov

					  for
					  
					  i 
					  
					  in
					  
					  range
					  
					  (
					  
					  pocet
					  
					  )
					  
					  :
    obdlznik
					  
					  ( s, 
					  polomer + s / 
					  
					  2
					  
					  )
					  
    k.
					  
					  left
					  
					  (
					  
					  360
					  
					  / pocet
					  
					  )
					  
#Kreslenie vnútorných 
					  kruhov
k.
					  
					  dot
					  
					  (
					  
					  2
					  
					  *
					  
					  polomer
					  
					  )
					  
k.
					  
					  color
					  
					  (
					  
					  "white"
					  
					  )
					  
k.
					  
					  dot
					  
					  ( s
					  
					  )
					  
p.
					  
					  mainloop
					  
					  (
					  
					  )

Vaše zaujímavé riešenia a najčastejšie chyby

Túto úlohu väčšina z vás vyriešila správne, v Imagine najkrajšie riešenie poslal tím nazov timu, oni dokonca určenie polomeru vnútorného kruhu riešili "roboticky", odmerali vnútornú vzdialenosť kolesa prechodom po jednom kroku cez nakreslené ozubené koleso a spočítali počet krokov. V Pythone najkrajšie riešenia poslali Šedá eminencia dodekahedrónov, tím krásny pstruh, LimeProgramming, Rúžové lentilky a Team.getName.

Niektorí ste zuby kreslili ako slnečné lúče s hrubou čiarou, namiesto obdĺžníkov ste kreslili polooblúky, no v tom prípade zuby nezapadnú do seba dobre. Preto sme vám nemohli prideliť body za správne zapadajúce zuby, kde je rovnaká šírka otvoru a zuba. Používanie parametrov všetci ste zvládli, čo nás veľmi potešilo.

Pozitívne hodnotíme, že ste prehľadne písali kódy programov a uviedli ste aj komentáre.

PALMA junior

Úloha o kreslení ozubených kolies