Autorské riešenie
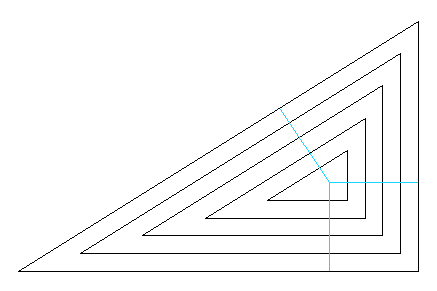
Podľa zadania máme nakresliť skupinu zadaného počtu pravouhlých trojuholníkov. Poznáme len rozmery odvesien najmenšieho trojuholníka, ktorý zachycuje prierez dreviny na konci prvého roku. Nasledovný obrázok znázorňuje prierez dreviny na konci piateho roku. Možno si všimnúť, že rastlina od začiatku až na koniec prvého roku vyrástla v každom smere o rovnakú vzdialenosť (nazvime ju hrúbkou vrstvy), čo platí aj pre ostatné roky.
Skupina do seba vnorených trojuholníkov s vyznačeným smerom rastu. V zadaní úlohy je uvedené, že hrúbka vrstvy je v každom roku rovnaká, len nie je uvedená ako zadaná hodnota. Na ďalšom obrázku si ukážeme, že hrúbku vrstvy vieme odvodiť zo zadaných dĺžok odvesien pravouhlého trojuholníka z prierezu dreviny na konci prvého roku.
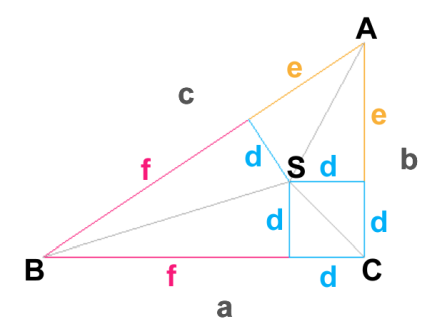
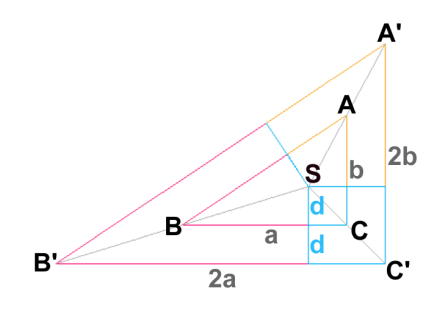
Trojuholníkový prierez na konci prvého roku - vzťahy medzi dĺžkami Bod S znázorňuje počiatok rastu dreviny, △ABC prierez dreviny na konci prvého roku. Z nákresu je zrejmé, že plocha △ABC je rovná súčtu plôch △ABS, △BCS a △CAS. a · b / 2 = c · d / 2 + a · d / 2 + b · d / 2 Ďalšou úpravou napokon vyjadríme hrúbku vrstvy d pomocou dĺžok odvesien a, b pravuhlého trojuholníka na konci prvého roku rastu.d · (a + b + c) = a · b d = a · b / (a + b + c) d = a · b / (a + b + √(a2+b2)) Jednotlivé trojuholníky budeme postupne vykresľovať od vrcholov pri pravých uhloch (pozri nasledovný obrázok). Vrchol pri pravom uhle vykresľovaného trojuholníka (△A'B'C') bude vzhľadom k vrcholu pri pravom uhle predchádzajúceho trojuholníka (△ABC) posunutý vodorovne vpravo o vzdialenosť hrúbky vrstvy a tiež zvisle nadol o vzdialenosť hrúbky vrstvy. Trojuholníky △ABC a △A'B'C' sú navzájom podobné. Dĺžky strán △A'B'C' sú dvakrát väčšie ako dĺžky strán △ABC. Dá sa to ukázať z podobnosti trojuholníkov △SBC a △S'B'C'. Výška v △SBC na stranu BC má dĺžku d a výška △S'B'C' na stranu B'C' má dĺžku 2·d. Rovnakou úvahou sa dá ukázať, že dĺžky strán trojuholníka po treťom roku budú (3·a, 3·b, 3·c) a po n-tom roku (n·a, n·b, n·c).
Vzťahy medzi dĺžkami strán trojuholníkov na konci 1. a 2. roka Na základe predchádzajúcich úvah vieme napísať funkciu hrubkaVrstvy, ktorá pre zadané hodnoty dĺžok odvesien vypočíta hrúbku vrstvy medzi susednými trojuholníkmi.Trojuholník reprezentujúci n-tý vek dreviny vykreslíme pomocou procedúry (resp. funkcie bez výsledku) trojuholník. Jej parametre sú dĺžky odvesien, dĺžka hrubky vrstvy a vek. Súradnice vrcholov trojuholníka sú nasledovné: (d·n, -d·n), (d·n, -d·n + b·n) a (d·n - a·n, -d·n). Napokon pomocou procedúry (resp. funkcie bez výsledku) prierez v cykle vykreslíme sústavu n trojuholníkov per zadané dĺžky odvesien a vek dreviny n. Riešenie úlohy v jazyku Imagine Logo môže vyzerať napríklad takto: ;Imagine Logo A riešenie úlohy v jazyku Python môže vyzerať napríklad takto:
#Python
import turtle, math
def hrubkaVrstvy(a, b):
'''
pre zadané dĺžky odvesien vypočíta hrúbku vrstvy
:param a: dĺžka 1. odvesny trojuholníka na konci 1. roku
:type a: float
:param b: dĺžka 2. odvesny trojuholníka na konci 1. roku
:type b: float
:rtype: float
'''
c = math.sqrt(a * a + b * b)
return a * b / (a + b + c)
def trojuholnik(a, b, d, vek):
'''
pre zadané dĺžky odvesien a vek vykreslí trojuholník
:param a: dĺžka 1. odvesny trojuholníka na konci 1. roku
:type a: float
:param b: dĺžka 2. odvesny trojuholníka na konci 1. roku
:type b: float
:param d: hrúbka vrstvy
:type d: float
:param vek: počet rokov dreviny
:type vek: int
'''
x0, y0 = d * vek, -d * vek
kor.penup()
kor.setposition(x0, y0)
kor.pendown()
kor.setposition(x0, y0 + b * vek)
kor.setposition(x0 - a * vek, y0)
kor.setposition(x0, y0)
def prierez(a, b, rokov):
'''
pre zadané dĺžky odvesien a počet rokov vykreslí prierez dreviny
:param a: dĺžka 1. odvesny trojuholníka na konci 1. roku
:type a: float
:param b: dĺžka 2. odvesny trojuholníka na konci 1. roku
:param rokov: počet rokov dreviny
:type rokov: float
'''
d = hrubkaVrstvy(a, b)
for i in range(1, rokov + 1):
trojuholnik(a, b, d, i)
kor = turtle.Turtle()
scr = turtle.Screen()
kor.speed(0)
kor.right(-90)
prierez(80, 50, 5)
scr.mainloop()
Táto súťažná úloha je zameraná na dôslednu analýzu matematického problému, na výpočty využívajúce podobnosť pravouhlých trojuholníkov, použitie Pytagorovej vety, na použitie stratégie dekompozície riešenia problému do riešenia podproblémov, na precvičenie použitia procedúr, resp. funkcií s parametrami, na precvičenie práce s príkazmi priradenia a opakovania. Vaše zaujímavé riešenia a najčastejšie chyby Do riešenia tejto úlohy sa, bohužiaľ, nezapojil žiaden súťažný tím z kategórie GURU. |
|||||||||