PALMA junior
Úloha o trénovacej ceste

Autorské riešenie
[stiahni]

• Počet riešiteľov: 3 / 8 = 75 %

• Úspešnosť riešenia: 3,33 / 8 = 42 %

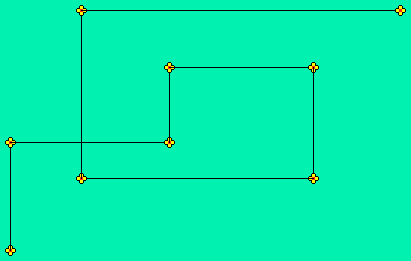
Podľa zadania úlohy máme vytvoriť náhodnú trénovaciu cestu v tvare lomenej čiary s pravými uhlami. V podmienkach úlohy je uvedené, že prvý úsek cesty je na sever (hore), počet kvetov je nepárne číslo, všetky náhodne vybrané kvety ležia v obdlžníku určenom prvým kvetom so súradnicami [0, 0] a posledným kvetom so zadanými kladnými súradnicami. Navyše sa požaduje, aby každú vybranú x-ovú a y-ovú súradnicu mali najviac 2 kvety cesty. Ilustračný príklad cesty uvedenej na obrázku v zadaní úlohy spĺňa všetky spomínané podmienky.

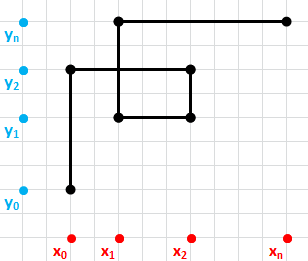
Veľmi užitočnou stratégiou riešenia tohto problému, je nakresliť ilustratívny alebo iný obrázok zodpovedajúci zadaniu úlohy a pozrieť sa na x-ové a y-ové súradnice bodov náhodnej lomenej čiary.

Pozorovaním obrázku môžeme dôsjť k nasledovným záverom:

1. prvý úsek lomenej čiary začína vo zvislom smere, posledný úsek vo vodorovnom smere,
2. zvislé a vodorovné úseky trasy sa striedajú,
3. pri nepárnom počte kvetov má trasa rovnaký počet zvislých a vodorovných úsekov,
4. všetky zvislé (resp. vodorovné) úseky trasy majú navzájom rôzne y-ové (resp. x-ové) súradnice,
5. nasledovný kvet má rovnakú x-ovú alebo y-ovú súradnicu s predchádzajúcim kvetom - pri vytváraní trasy budeme opakovane pridávať najprv kvet s rovnakou x-ovou súradnicou a za ním kvet s rovnakou y-ovou súradnicou,
6. počet rôznych x-ových súradníc je rovnaký ako počet rôznych y-ových súradníc kvetov,
7. x-ové (resp. y-ové) súradnice všetkých kvetov ležia v intervale hodnôt medzi x-ovými (resp. y-ovými) súradnicami prvého a koncového bodu.

Pri vytváraní súradníc postupnosti kvetov určujúcich trasu medzi prvým a koncovým kvetom budeme postupovať nasledovne.

Najprv vytvoríme zoznam x-ových (resp. y-ových) súradníc pre všetky kvety. Len prvý kvet má jedinečnú y-ovú súradnicu, každá ďalšia dvojica bodov za ním má rovnakú y-ovú súradnicu. Podobne posledný kvet má jedinečnú x-ovú súradnicu, každá dvojica predchádzajúcich bodov pred ním má rovnakú x-ovú súradnicu. Zoznam rôznych x-ových a zoznam rôznych y-ových súradníc kvetov sú rovnako veľké a pre zadaný celkový počet kvetov počet majú (počet+1)/2 prvkov. Program na vytvorenie zoznamu s daným počtom rôznych x-ových a zoznamu s y-ovými súradnicami môže vyzerať nasledovne:

Z vytvorených zoznamov s náhodnými x-ovými a y-ovými súradnicami môžeme zostaviť zoznam súradníc kvetov - uzlov pravouhlej lomenej čiary, a to pridávaní dvojíc nasledovných bodov. Prvý z nich má rovnakú x-ovú súradnicu ako predchádzajúci bod a inú y-ovú súradnicu ako predchádzajúci bod a druhý bod bude mať inú x-ovú súradnicu ako prvý bod dvojice a rovnakú y-ovú súradnicu ako prvý bod dvojice. Časť programu na zostavenie zoznamu súradníc kvetov (uložených v globálnej premennej "cesta) môže vyzerať nasledovne:

V procedúre na vykreslenie cesty (lomenej čiary) sa postupne prechádza zoznamom súradníc cesty (uložených v premennej "cesta), mení poloha korytnačky na tieto súradnice, kde sa následne odtlačí tvar korytnačky (kvet):

Ešte do procedúry vytvorCestu doplníme podmienky riešiteľnosti úlohy - ošetríme hodnoty vstupných parametrov (súradníce koncového bodu musia byť kladné a musia sa zmestiť na obrazovku, počet kvetov musí byť nepárne číslo, počet kvetov musí byť aspoň 3, počet generovaných x-ových a y-ových súradníc musí byť nanajvýš polovica z možného počtu bodov):

Po doplnení ošetrenia hodnôt vstupných parametrov a vytvorenia zoznamu súradníc kvetov dostaneme výslednú podobu procedúry vytvorCestu:

Náročnejšou podobou tejto úlohy je úloha 4 z tohto finálového kola, v ktorej počet kvetov nie je obmedzený na nepárne čísla, nie je určený smer kreslenia trasy z prvého kvetu na sever, súradnice prvého kvetu nie sú [0,0], ale zadané ako ďalší vstupný parameter.

Táto súťažná úloha je zameraná na použitie stratégií riešenia problémov - rozloženie problému do podproblémov, nakreslenie si obrázku, dôsledný rozbor možných prípadov riešenia úlohy, a tiež na výpočty s karteziánskymi súradnicami, použitie príkazov opakovania, vetvenia, zložených podmienok (so spojkami zároveň, alebo), údajového typu jednoduchý aj vnorený zoznam, algoritmus generovania náhodných čísel podľa zadaných pravidiel.

Vaše zaujímavé riešenia a najčastejšie chyby

Do riešenia tejto úlohy sa zapojili 3 zo 4 tímov finalového kola. Z toho len 2 tímy mali čiastočne správne riešenia. Celkové priemerné skóre tejto úlohy bolo 2,5 bodu, čo je cca 31% úspešnosť.

Nedostatky, ktoré sme našli v riešeniach súťažiacich:

• programy nevykresľovali správny počet kvetov, prípadne chýbal vstupný parameter určujúci počet kvetov,
• kreslenie kvetov aj mimo obdĺžnikovej plochy určenej prvým a koncovým kvetom,
• žiadne alebo len čiastočné ošetrenie vstupných parametrov.