PALMA junior
Úloha o tom ako korytnačky budovali diaľnice

Autorské riešenie
[stiahni]

• Počet riešiteľov: 5 / 11 = 45,5 %

• Úspešnosť riešenia: 3,8 / 8 = 47,5 %

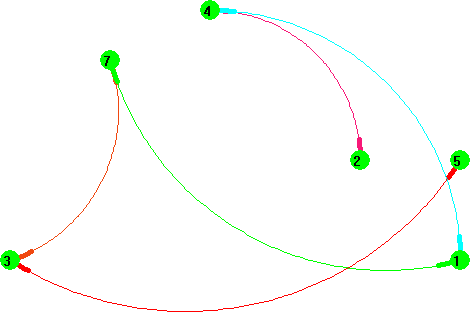
Nájsť riešenie tejto úlohy veru nie je jednoduché. Musíme zistiť, či existuje diaľničná trasa medzi zadanými mestami. Ak áno, musíme ich nájsť všetky. Navyše nesmieme do žiadneho mesta vojsť viac ako raz. A všetko čo máme k dispozícii je len zoznam diaľnic - zoznam dvojíc miest medzi ktorými je priame diaľničné spojenie.

Skúsme si na chvíľu predstaviť, ako by sme hľadali cestu z nášho mesta do vybraného dovolenkového miesta. Zrejme by sme začali tým, že vyberieme nejakú cestu z nášho mesta. Najlepšie tú, ktorá aspoň približne smeruje k cieľu. Skúsili by sme po nej prejsť do ďalšieho mesta. A tam by sme postup zopakovali. Opäť by sme vybrali nejakú cestu, ktorá smeruje k nášmu cieľu a nie je to tá, po ktorej sme prišli. Takto by sme postupovali kým by sme sa nedostali do cieľa cesty.

Fungoval by takýto postup? Asi nie vždy. Pozrime si nasledujúci obrázok a predstavme si, ako by sme hľadali cestu z mesta 1 do mesta 5.

V meste 1 by sme si zrejme vybrali cestu do mesta 4. V meste 4 už nemáme na výber a jediná cesta, ktorou môžeme pokračovať je cesta do mesta 2. Tu je situácia ešte horšia, lebo odtiaľto sa už nikam nedostaneme. Čo teraz?

Mohli by sme sa vrátiť do predchádzajúceho mesta a vybrať si nejakú inú, ešte nevyskúšanú cestu a pokračovať ňou. Inak povedané, ak sa už nedá z nejakého mesta pokračovať ďalej, vráť sa do predchádzajúceho mesta a vyber sa nejakou, ešte nevyskúšanou cestou. Ak taká už nie je, vráť sa o ďalší krok. Keďže chceme nájsť všetky trasy, má zmysel skúsiť v každom meste všetky cesty. Aj keď sme nejakú trasu už našli, aj tak je ešte potrebné hľadať či existujú nejaké ďalšie.

Uvedomme si ešte jednu dôležitú vec. Keď si vyberieme nejakú cestu v danom meste, zostáva nám vyriešiť podobný problém ako na začiatku. Zmenila sa len štartovacia pozícia. Teda problém, či existuje trasa z mesta 1 do mesta 5 vyriešime tak, že vyriešime jednoduchšie problémy:

existuje trasa z mesta 4 do mesta 5? ak sme sa v meste 1 vybrali cestou do mesta 4

a

existuje trasa z mesta 7 do mesta 5? ak sme sa v meste 1 vybrali cestou do mesta 7

Väčší problém sme teda nahradili niekoľkými podobnými, ale menšími. Pri nich budeme postupovať rovnako a nahradíme ich ešte menším. Je jasné, že takto to nemôžeme robiť do nekonečna. Otázka znie, či vieme niektoré z týchto problémov vyriešiť hneď. Odpoveď je áno.

Ak máme hľadať cestu z mesta do toho istého mesta, odpoveď je áno, trasa existuje.

Ak už neexistuje v meste žiadna cesta na vyskúšanie, vrátime sa do predchádzajúceho mesta.

Prvá verzia procedúry existujeTrasa by mohla vyzerať nasledovne: 

Ak :od = :do, zistili sme, že trasa existuje. Zatiaľ však nevieme cez ktoré mestá vedie.

V opačnom prípade vyskúšame všetky cesty, ktorých jeden koncový bod je v aktuálnom meste (:od).

Naša procedúra ešte nie je úplná. Nevieme odpovedať na otázku, kadiaľ vedie nájdená trasa. Zároveň nám nič nebráni v tom, aby sme nejaké mesto navštívili viac krát. Ak z aktuálneho mesta vedie cesta do mesta v ktorom sme už boli, skúsime ju. Musíme teda zabezpečiť, aby sme vždy vedeli ktoré mestá a v akom poradí sme už navštívili. Dosiahneme to jednoducho. Okrem parametrov :od a :do pošleme procedúre aj zoznam už navštívených miest. Upravená verzia procedúry existujeTrasa môže vyzerať takto:

Na začiatku je zoznam miest (:navstiveneMesta) prázdny. V aktuálnom meste k nemu pridáme názov mesta a takto doplnený ho pošleme ako parameter ďalej. Všimnime si aj to, že nejakú cestu použijeme len vtedy, ak smeruje do mesta, v ktorom sme ešte pri prechode práve skúmanou trasou neboli.

Vaše zaujímavé riešenia a najčastejšie chyby

Najväčši problém vám robilo nájdenie algoritmu na hľadanie trasy. Niektorí z vás prišli na myšlienku rekurzívneho prehľadávania ale nevedeli ju celkom úspešne implementovať. Takmer správne riešenie mal tím Expert JM&JM. Jedinou chybou bol nespravny /nekompletný/ výpis nájdených trás.