PALMA junior
Úloha o hre farebné sudoku

Autorské riešenie
[stiahni]

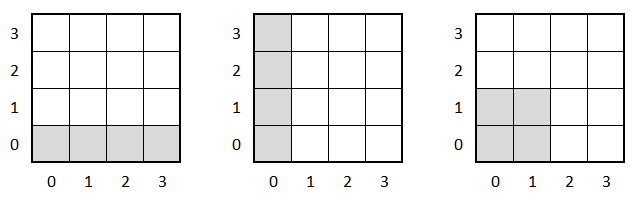
Najprv si nakreslíme obrázky herného plánu sudoku, pomocou ktorých postupne prídeme na to, ako máme prechádzať všetkými oblasťami, ktoré potrebujeme otestovať, či obsahujú všetky zadané farby. Pri overovaní riešenia sudoku sa testujú riadky, stĺpce a štvorcové oblasti.

Očíslujeme riadky a stĺpce hracieho plánu sudoku celými číslami od 0 do 3. Postupne otestujeme:

• riadky
  • obdĺžnikovú oblasť od štvorčeka [0,0] do štvorčeka [3,0]
  • obdĺžnikovú oblasť od štvorčeka [0,1] do štvorčeka [3,1]
  • obdĺžnikovú oblasť od štvorčeka [0,2] do štvorčeka [3,2]
  • obdĺžnikovú oblasť od štvorčeka [0,3] do štvorčeka [3,3]
• stĺpce
  • obdĺžnikovú oblasť od štvorčeka [0,0] do štvorčeka [0,3]
  • obdĺžnikovú oblasť od štvorčeka [1,0] do štvorčeka [1,3]
  • obdĺžnikovú oblasť od štvorčeka [2,0] do štvorčeka [2,3]
  • obdĺžnikovú oblasť od štvorčeka [3,0] do štvorčeka [3,3]
• štvorcové oblasti
  • obdĺžnikovú oblasť od štvorčeka [0,0] do štvorčeka [1,1]
  • obdĺžnikovú oblasť od štvorčeka [0,2] do štvorčeka [1,3]
  • obdĺžnikovú oblasť od štvorčeka [2,0] do štvorčeka [3,1]
  • obdĺžnikovú oblasť od štvorčeka [2,2] do štvorčeka [3,3]

Vidíme, že testujeme vždy obdĺžnikové oblasti veľkosti 4 štvorčekov, ktoré začínajú a končia v štvorčekoch s uvedenými súradnicami. Predstavme si, že vieme otestovať každú z oblasti pomocou jednej funkcie overOblasť, ktorej výsledkom je hodnota "áno, ako oblasť obsahuje všetky zadané farby, resp. "nie, ak chýba niektorá farba. V procedúre over_riešenie na začiatku nastavíme premennú "chyby na 0 a pri každom negatívnom výsledku testovania ju zvýšime o 1. Po otestovaní všetkých oblastí prehlasíme, že vyfarbený hrací plánik je riešením sudoku, ak nebolo žiadne z testovaní negatívne. Procedúra over_riešenie by mohla vyzerať nasledovne:

Teraz si ukážeme ako naprogramovať funkciu overOblasť, ktorá otestuje obdĺžnikovú oblasť určenú dvojicou štvorčekov [x0,y0] a [x1,y1]. Pri oblastiach s jedným riadkom, resp. jedným stĺpcom by stačilo na ich otestovanie použiť jeden cyklus. Pri testovaní štvorcových oblastí musíme použiť dva cykly, ktoré sa dajú použiť aj pri jednoriadkových, resp. jednostĺpcových oblastiach (vnútorný, resp. vonkajší cyklus sa vykonajú len raz). V tele vnorených cyklov sa budeme presúvať na všetky súradnice štvočekov zadanej oblasti a do zoznamu - premennej "farby budeme postupne pridávať farby všetkých štvorčekov zadanej oblasti. Na konci len otestujeme usporiadaný zoznam prečítaných farieb so zoznamom farieb [modrá zelená žltá červená]. Funkcia overOblasť so štyrmi parametrami :x0 :y0 :x1 :y1 môže vyzerať nasledovne:

Uvedené riešenie úlohy je prvoplánové, dá sa viac zovšeobecniť. Vo všeobecnejšom riešení zadáme ako parametre procedury - rozmer hracieho plánu sudoku, veľkosť štvorčeka, zoznam testovaných farieb. Poďme teraz určiť, aké rozmery hracích plánov môže mať hra sudoku. Pri testovaní riešenia sudoku musí mať každý riadok, stĺpec aj štvorcová oblasť rovnaký počet prvkov. Označme si písmenom n počet riadkov (stĺpcov, štvorcových oblastí) a písmenom v šírku, resp výšku štvorcovej oblasti. Štvorcová oblasť s rozmermi v×v štvorčekov obsahuje n štvorčekov. Aby bolo v celé číslo, musí byť číslo n druhou mocninou celého čísla, napr. 4, 9, 16, 25... Všeobecnejšie riešenie procedúry overRiešenie s parametrami vyzerá nasledovne:

Vo funkcii overVšetko postupne prechádzame riadkami, stĺpcami a štvorcovými oblasťami. Výpočet sa ukončí pri prvej oblasti, kde je výsledok testovania negatívny. Funkcia overVšetko vyzerá nasledovne:

Funkcia overOblasť s parametrami vyzerá nasledovne:

Ďalším zovšeobecnenie riešenia úlohy by bolo zistenie si všetkých parametrov hracieho plánu sudoku (rozmeru hracieho plánu sudoku, zoznamu farieb, veľkosti štvorčeka) postupným prechádzaním obrázka bod po bode. Skoršie ukončenie výpočtu môžeme dosiahnuť, ak počas prechádzania jednotlivými štvorčekmi vybranej oblasti, testujeme, či práve načítaná farba štvorčeka nie je v zozname farieb už prejdených štvorčekov vybranej oblasti.

Táto súťažná úloha je zameraná na použitie stratégií riešenia problémov - rozlož problém do podproblémov, nakresli si obrázok/tabuľku, najdi vzor a tiež na výpočty s karteziánskymi súradnicami, použitie príkazov opakovania, vetvenia, funkcií, údajového typu zoznam. Riešenie tejto úlohy sa dá využiť pri reálnom sudoku skeneri zostaveného z robotických stavebníc s využitím farebného svetelného senzoru a dvoch servomotorov.

Vaše zaujímavé riešenia a najčastejšie chyby

Do riešenia tejto úlohy pre expertov sa zapojilo 15 tímov. Len 2 tímy vyriešili túto úlohu na plný počet bodov - ikztzu, Nezapamatatelny, ktorým gratulujeme.

V riiešeniach tejto úlohy sa vyskytli rôzne prístupy ako

• prechádzať oblasťami:
  • s použitím korytnačej grafiky (s návratom na začiatok oblasti, resp. hadovite bez návratu),
  • s použitím karteziánskej grafiky s presunom priamo na štvorcové políčka s vypočítanými súradnicami,
• kódovať farby štvorčekov:
  • prirodzene ich názvami ("žltá, "zelená, "modrá, "červená),
  • pomocou kódovania mocninami čísla 10, či desatinnými číslami,
• vyhodnocovať testy v oblastiach
  • súčet hodnôt farieb,
  • rôznosť hodnôt farieb (toto funguje len, keď je celkový počet farieb v obrázku nanajvýš 4, pri 16 rôznych farbách to dá nesprávny výsledok),
• optimalizovať ukončenie výpočtu:
  • prejdenie všetkými oblasťami,
  • ukončenie výpočtu pri prvej oblasti s negatívnym výsledkom,
  • ukončenie výpočtu pri prvom políčku, ktorého farba je zhodná s niektorou zo zoznamu farieb už prečítaných štvorčekov v niektorej oblasti.

V jednom riešení autori načítali celú hraciu plochu sudoku do jednej premennej ako zoznam zoznamov, ktorý potom postupne vyhodnocovali.

Nedostatky, ktoré sme našli v riešeniach súťažiacich:

• riešenie sudoku len pre prípad sudoku s rozmermi 4×4,
• testovanie len riadkov a stĺpcov, nie štvorcových oblastí, čo je riešením redukovanej úlohy - overovanie, či daná schéma predstavuje latinský štvorec,
• neuvedenie, alebo chybné uvedenie možného rozmeru sudoku,
• neukončenie výpočtu pri prvej chybnej oblasti, ale prechádzanie úplne všetkými oblasťami,
• neprehľadný kód s opakujúcimi časťami kódov, kde by pomohli cykly, či procedúry,
• použitie nemnemotechnických premenných - jednopísmenové, čí číselné (napr. :a, :1).