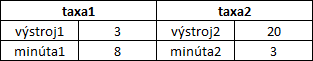PALMA junior
Úloha o tom ako korytnačky trénovali lyžovanie

Autorské riešenie
[stiahni]

Pri riešení tejto úlohy si zoberieme na pomoc matematiku. Aby sme vedeli posúdiť taxy, predstavme si tabuľku, v ktorej by boli všetky možné dĺžky tréningov v minútach. Pri každej minúte by bolo uvedené, koľko by sme zaplatili ,ak by sme použili taxu 1 a koľko by sme zaplatili, ak by sme použili traxu 2. Stačilo by sa pozrieť do tabuľky a hneď by sme vedeli, ktorá taxa je pre nás výhodnejšia. Zostrojme si takúto tabuľku pre nasledovné taxy:

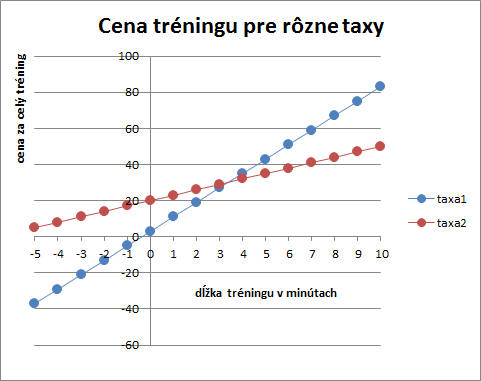
Takáto tabuľka by však obsahovala píliš veľa čísiel a ťažko by sa v nej orientovalo. Bola by dosť neprehľadná. Našťastie existuje riešenie. Údaje z tabuľky vieme vykresliť v grafe.

Všimnime si na grafe niekoľko zaujímavých vecí:

• na osi x je dĺžka tréningu v minútach, na osi y je cena tréningu, modré, resp. červené kolieska znázorňujú, koľko stojí tréning v taxy 1, resp. v taxy 2 pre danú dĺžku tréningu,

• body, ktoré predstavujú ceny tréningov v jednej taxy ležia na jednej priamke,

• tam, kde sú body jednej taxy nižšie ako body druhej, je táto taxa výhodnejšia,

• tam, kde sa priamky stretnú, sú obe taxy rovnako výhodné,

• na grafe sú zobrazené aj záporne hodnoty minút, tie sa však reálne nedajú dosiahnuť,

• v nultej minúte je výhodnejšia tá taxa, ktorá má nižšiu cenu za výstroj,

• cena tréningu v danej taxy rastie rýchlejšie, ak zvýšime cenu za minútu.

Matematika je v tomto prípade užitočná aj v tom, že môžeme rozhodnúť o tom, ktorá taxa je výhodnejšia a to aj bez toho, aby sme videli predchádzajúcu tabuľku alebo graf. Stačí, ak správne využijeme vlastnosti a vzájomnú polohu modrej a červenej "priamky" (v skutočnosti sú to len izolované body). Na to nám stačí zistiť, kde sa dané priamky pretnú a ktorá stúpa strmšie.

Strmosť priamky je určená cenou za minútu tréningu. Čím je cena za minútu vyššia, tým je priamka strmšia. Prienik priamok, rovnosť oboch táx, vypočítame nasledovne:

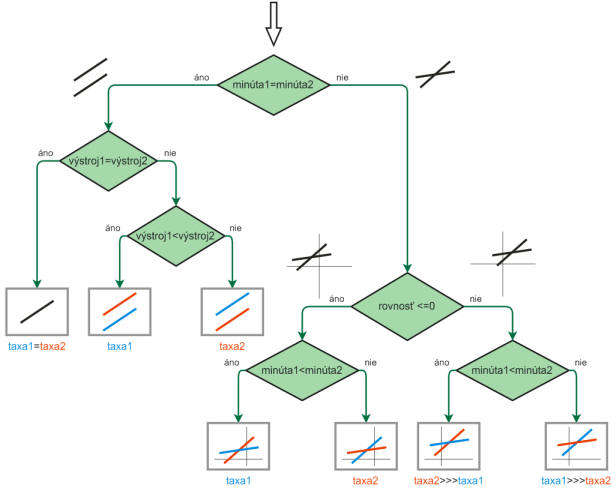
výstroj1 + minúta1 x rovnosť = výstroj2 + minúta2 x rovnosť
minúta1 x rovnosť - minúta2 x rovnosť = výstroj2 - výstroj1
rovnosť x (minúta1 - minúta2)= výstroj2 - výstroj1
rovnosť = (výstroj2 - výstroj1) / (minúta1 - minúta2)

Pozornejší z vás si isto všimli, že v prípade ak budú priamky rovnobežné je takýto výpočet nemožný. Výraz minúta1 - minúta2 je rovný 0 a nulou sa deliť nedá. V tomto prípade minúta, kedy by boli taxy rovnako výhodné buď neexistuje (priamky sú rôzne) alebo naopak, taxy sú rovnako výhodné v každej minúte (priamky sú totožné).

Pri rozhodovaní, kedy je ktorá taxa výhodnejšia nám pomôže nasledovný rozhodovací strom. Po každom rozhodnutí je znázornená vzájomná poloha priamok (čierne priamky), resp. vzťah medzi taxou 1 (modrá) a taxou 2 (červená).

Najskôr zistíme, či sú priamky rovnobežné (minúta1=minúta2). Následne, či sú totožné (výstroj1=výstroj2) resp. ktorá je umiestnená vyššie (výstroj1<výstroj2).

Ak priamky nie sú rovnobežné, zisťujeme, kde je ich prienik: pred osou y (rovnosť<0) alebo za ňou. Ak je prienik pred osou y, zistíme ktorá priamka je strmšia (minúta1<minúta2). Ak je prienik za osou y, na základe strmosti (minúta1<minúta2) zistíme, ktorou taxou je výhodnejšie začať a ktorou neskôr (po prieniku priamok) pokračovať.

Rozhodovací strom prepísaný do jazyka Logo môže vyzerať nasledovne:

Vaše zaujímavé riešenia a najčastejšie chyby

Túto úlohu vyriešili správne len dva tímy: Expert JM&JM a Expert Béčka. Blahoželáme.

Ostatné tímy buď nesprávne pochopili zadanie a snažili zistiť, ktorá trať je výhodnejšie alebo ktorá taxa je výhodnejšia pre šprintérov a ktorá pre vytrvalcov.

O tratiach nemá zmysel uvažovať, lebo nevieme, ako rýchlo pretekári bežia. Rovnako ani o vytrvalcoch a šprintéroch nemá zmysel uvažovať, lebo nevieme dĺžku ich trate ani čas ich tréningu.

Niektorí zisťovali, ktorá taxa je výhodnejšia pre zadanú konkrétnu dĺžku trvania tréningu. Tu však nezistili odpoveď na otázku "ktorá taxa a kedy je výhodnejšia?" Zistili to len pre jednu, konkrétnu dĺžku trvania tréningu.