PALMA junior
Úloha o pancierovačke

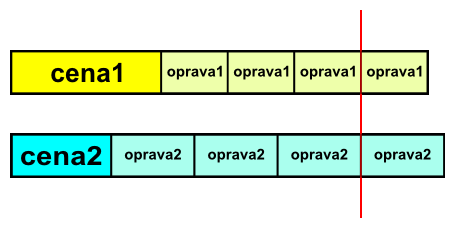
Autorské riešenie
[stiahni]

Pri riešení úlohy musíme najprv určiť vstupy - vstupné parametre procedúry. Zo zadania vieme, že máme dve pancierovačky a každá z nich má nákupnú cenu a náklady na opravu jedného panciera. Označme cenu prvej pancierovačky premennou cena1 a náklady na opravu oprava1. Podobne označíme cenu druhej pancierovačky premennou cena2 a náklady na opravu oprava2. Pre lepšiu názornosť si nakreslíme pomocný obrázok. Celkové náklady prvej pancierovačky znázorníme pomocou obdlžníkov - prvý obdlžník bude predstavovať nákupnú cenu určenú premennou cena1 a ďalšie obdlžníky náklady na opravu viacerých pancierov určené premennou oprava1. Podobne pod tieto obdlžníky znázorníme obdlžníky predstavujúce celkové náklady druhej pancierovačky. Na obrázku je znázornená situácia pre hodnoty premenných:
cena1=18, oprava1=8, cena2=12, oprava2=10.

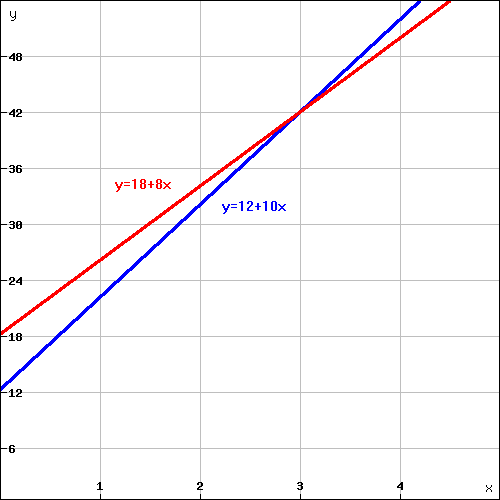
Podľa príkladu z obrázku je zrejmé, že ak by sme neopravili žiaden pancier alebo 1, či 2 panciere, oplatí sa kúpiť druhú pancierovačku. Pri 3 opravených pancieroch majú obe pancierovačky rovnaké celkové náklady. Pri 4 a viacerých opravených pancieroch sa oplatí kúpiť prvú pancierovačku. Výsledok riešenia tejto úlohy bude teda závisieť aj od počtu opravených pancierov.

V nasledovnom riešení použijeme 5 parametrov, premenné cena1, oprava1, cena2, oprava2 a piaty parameter - premennú kusov, ktorá predstavuje počet opravených pancierov. Riešenie úlohy je jednoduché. Najprv spočítame celkové náklady prvej a druhej pancierovačky, potom tieto čísla porovnáme a podľa výsledku ich porovnania vypíšeme patričný komentár ku všetkým trom možnostiam kúpy prvej, či druhej pancierovačky. Riešenie úlohy môže vyzerať nasledovne:

Uvedené riešenie poskytne správne výsledky pre rôzne zadané hodnoty prvej a druhej pancierovačky, bez ohľadu na to, či je niektorá z nich drahšia, či lacnejšia od druhej z nich.

Túto úlohu môžme riešiť aj tak, že vystačíme len so štyrmi parametrami, ktoré predstavujú premennné cena1, oprava1, cena2, oprava2. Potrebujeme však nájsť hraničnú medzu počtu opravených pancierov. Pod touto medzou sa oplatí kúpiť jednu pancierovačku a nad medzou druhú pancierovačku. Ak hodnota medze je celé číslo, tak je jedno ktorú z pancierovačiek kúpime. Medzu vypočítame z rovnice:

cena1 + oprava1 · medza = cena2 + oprava2 · medza

medza = (cena1 - cena2) / (oprava2 - oprava1)

Ak chceme dôsledne dodržať podmienky zadania úlohy, ošetríme vstupy. Výpočet zastavíme s komentárom o chybnom (nevyhovujúcom) vstupe, ak nebude platiť ani jedna z uvedených podmienok:

cena1 > cena2  A ZÁROVEŇ  oprava1 < oprava2

cena1 < cena2  A ZÁROVEŇ  oprava1 > oprava2

Riešenie úlohy môže vysledovať nasledovne:

Ak poznáme lineárne funkcie, môžme celkové náklady pancierovačiek v závislosti od počtu opravených pancierov znázorniť v súradnicovej sústave ako dve lineárne funkcie. Jedna z funkcii pretína os y vyššie ako druhá funkcia, ale rastie pomalšie. Keďže sú navyše obidve rastúce, pretnú sa v niektorom bode, ktorý bude medznou hodnotou. Na dolnom obrázku sú zobrazené dve funkcie predstavujúce konkrétny príklad uvedený na začiatku tohto autorského riešenia. Celkové náklady prvej pancierovačky reprezentuje funkcia y=18+8x a celkové náklady druhej pancierovačky funkcia y=12+10x. Do medznej hodnoty x=3 (opravených pancierov) sa oplatí kúpiť lacnejšiu pancierovačku s nákupnou cenou 12. Pri medznej hodnote 3, ktorá je celým číslom, je možné kúpiť hociktorú z týchto pancierovačiek. Pri hodnote viac ako 3 sa oplatí kúpiť drahšiu pancierovačku s nákupnou cenou 18.

Zadanie úlohy je otvorené, čo umožňuje premyslieť aj ďalšie vstupné parametre. Okrem nákupnej ceny pancierovačiek a nákladov na opravu panciera sa dá uvažovať aj o nákladoch na pravidelné servisné prehliadky po určitom počte opravených pancierov a prípadné opravy pancierovačky v závislosti od jej kvality (menšej, či väčšej poruchovosti).

Vaše zaujímavé riešenia a najčastejšie chyby

Úlohu riešilo 12 tímov. Až na jeden tím, ktorý použil len 4 vstupné parametre, ostatné tímy použili 5 parametrov. Súťažiaci Michal Bali dokonca uviedol riešenie s 9 parametrami, kde uvažoval aj opravy pancierovačiek, za čo ho veľmi chválime.

Najčastejšie nedostatky, ktorých ste sa dopustili vo svojich riešeniach:

• neošetrovali ste vstupy, či vyhovujú podmienke zadania úlohy (urobilo tak, len 4 tímy - Bali, JM&JM, Nezapamatatelny, nnn)
• pri výstupoch ste neuvažovali prípad nastania rovnosti - odpoveď, že pre určitý počet opráv je možné kúpiť hociktorú z pancierovačiek

Ďalšie naše p ostrehy a odporúčania:

• V jednom prípade súťažiaci nepoužili žiadne vstupné parametre, ale načítavali ich postupne pomocou operácie vstupu čitajSlovo, čo je menej typické. Pohodlnejšie pre používateľa je použiť vstupné polia, do ktorých zadá patričné hodnoty. Niektoré tímy použili vstupné a výstupné polia na grafickej obrazovke, ale niektorí zabudli dať tlačidlo na spustenie procedúry.
• Odporúčame čo najmenej používať globálne premenné (namiesto príkazu priradenia UROB používajte príkaz UROBTU, ktorým priraďujete hodnotu do lokálnej premennej). Pri programovaní náročnejších programov s viacerými procedúrami, by každá z nich mohla zmeniť globálnu premennú, čo prináša väčšie problémy pri odhaľovaní chýb. Držme sa pravidla, to čo nemusí byť verejne dostupné (globálne), nech je privátne (lokálne).
• Niektorí súťažiaci nepoužívate prehľadný zápis programu, čo môže byť zdrojom chýb, skúste si pozrieť autorské riešenia tejto, či iných úloh, kde sa snažíme programy zapisovať tak, aby bolo jasné, kde ktorý príkaz končí a príkazy rovnakej úrovne, aby boli odsadené pekne pod sebou. Pochvalu za úpravu programu (odsadenie, komentáre, mená premenných, atď.) si zaslúžia tímy - JM&JM, lupa, Michal Bali, nnn, Nezapamatatelny, Zoltán Hanesz Michal Pándy