PALMA junior
Úloha o vykopávkach

Autorské riešenie
[stiahni]

Cieľom úlohy bolo vykresliť všetky štvorce, ktorých vrcholy ležia v bodkovej mriežke, pričom dva vrcholy štvorca poznáme (vykreslia sa červenou farbou).

Úlohu je možné riešiť "skusmo" pomocou korytnačky, s ktorou vycestujeme a budeme odhadovať pomocou uhlov a vzdialeností, kde sa hľadané štvorce nachádzajú. Pekné riešenie napísal jeden zo súťažiacich Michal Bali , ktorý zvolil takýto prístup.

My však zvolíme matematický prístup - pokúsime sa vypočítať súradnice hľadaných bodov, ktoré budú spolu s pôvodnými tvoriť vrcholy štvorca a potom ich už len "obskáčeme" pomocou korytnačky.

Riešenia rozdelíme na dve skupiny:
1. ak dva červené body tvoria stranu hľadaného štvorca
2. ak dva červené body tvoria uhlopriečku hľadaného štvorca

V programe najprv zabezpečíme, aby bod so súradnicami [x1 y1] bol "naľavo" od bodu so súradnicami [x2 y2].

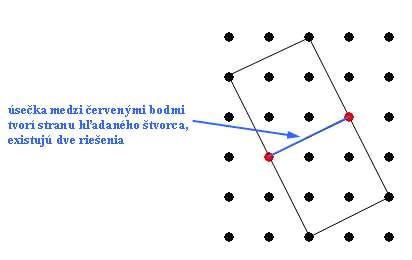
Najskôr sa zamerajme na 1. skupinu riešení, teda keď dva červené body spojíme, dostaneme stranu hľadaného štvorca. Teraz si stačí uvedomiť, že štvorec je možné hľadať v dvoch kolmých smeroch od zostrojenej úsečky, teda existujú dve riešenia.

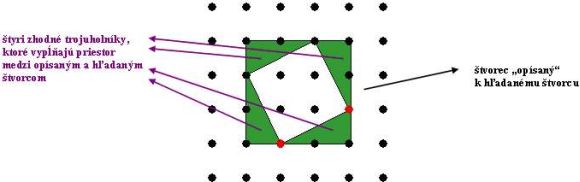
Existenciu riešenia zaručuje fakt, že výslednému štvorcu je možné "opísať" štvorec, ktorý bude mať strany rovnobežné so stranami papiera. Potom zistíme, že priestor medzi opísaným štvorcom a hľadaným štvorcom vypĺňajú štyri zhodné trojuholníky, len pootočené.

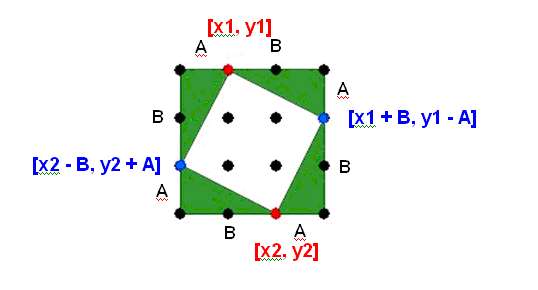
Ak nájdeme tieto štyri trojuholníky, nájdeme aj hľadaný štvorec. Teda ku akejkoľvek dvojici červených bodov existujú dve riešenia (samozrejme za predpokladu, že sa zmestia do našej obmedzenej bodkovej mriežky). Pozrime sa bližšie na tento obrázok:

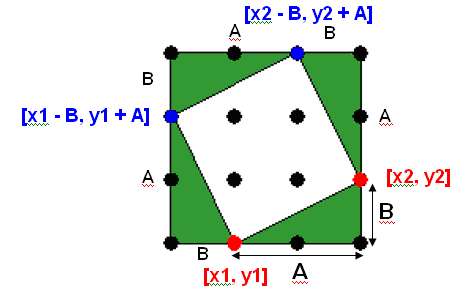
Keď si označíme strany zelených trojuholníčkov ako A,B, tak vidíme, že A vieme vypočítať ako rozdiel medzi x-ovými súradnicami červených bodov, B vieme vypočítať ako rozdiel medzi y-ovými súradnicami červených bodov. Môžeme teda písať:

Súradnice zvyšných dvoch vrcholov štvorca vypočítame podľa vzťahov z obrázka. Symetricky si vieme odvodiť vzťah pre výpočet súradníc vrcholov pre štvorec v opačnom smere.

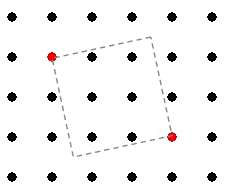
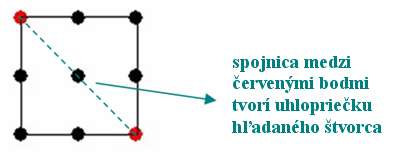
2.skupina prípadov je zapeklitejšia - ak dva vyznačené červené body tvoria uhlopriečku daného štvorca. Riešenie totiž nemusí existovať vždy. Napríklad pre takto zvolené dva body riešenie neexistuje (štvorec samozrejme existuje, ale jeho zvyšné dva vrcholy neležia v mriežke bodov):

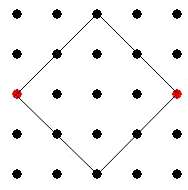
Ľahko nahliadnuteľné riešenie je, keď rozdiel medzi x-ovými a y-ovými súradnicami červených bodov je rovnaký, napríklad:

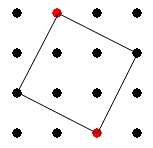
Avšak aj za iných okolností existuje štvorec, v ktorom červené body budú tvoriť jeho uhlopriečku, napríklad:

alebo

Potrebovali by sme teda určiť podmienku, kedy riešenie existuje. Použijeme podobnú "fintu", ako v predchádzajúcom príklade:

Ak si znova označíme veľkosti strán trojuholníkov ako A a B, tak na základe toho vieme dopočítať súradnice zvyšných dvoch vrcholov. Ako ale vypočítame A a B? Všimnite si, že v tomto prípade sa rozdiel y-ových súradníc (rozdielY) rovná súčtu A+B a rozdiel x-ových súradníc (rozdielX) sa rovná rozdielu A-B, z čoho máme, že:

Keďže A a B musia byť celé čísla, tak oba čitatele musia byť párne čísla (aby po vydelení dvoma vyšlo celé číslo). Súčet (rozdiel) dvoch čísel je párny iba vtedy, ak sú oba sčítance párne (napr. 2 + 4 je párne číslo) alebo sú oba sčítance nepárne (napr. 3 + 5 je párne číslo). Teda podmienkou k tomu, aby zadané dva body mohli tvoriť uhlopriečku hľadaného štvorca, je, že rozdielX musí mať rovnakú paritu ako rozdielY (buď sú obe párne alebo oba nepárne).

Poznámka: teraz sme pod rozdielomX a rozdielomY mysleli nie reálnu súradnicovú vzdialenosť, ale "bodkovú vzdialenosť", tj. napr. na poslednom obrázku je rozdiel x-ových súradníc 1 a rozdiel y-ových súradníc 3 - obe sú nepárne. Ak vieme, že vzdialenosť medzi dvoma susednými bodkami je 40, tak v programe podmienku overíme nasledovne:

Aby bolo riešenie úplné, musíme ešte ošetriť symetrický prípad (keď na predchádzajúcom obrázku nemáme "horný" a "dolný bod", ale dva bočné) a tiež si treba dávať pozor na to, či naozaj ten "horný" bod má súradnice x1 y1 a nie x2 y2 (tj. horizontálne otočený obrázok).

Vaše zaujímavé riešenia a najčastejšie chyby

Úlohu riešilo najviac tímov tohto kola. Nie všetci však prišli na to, že môžu existovať až tri riešenia (dve riešenia, ak dva červené body tvoria stranu štvorca a jedno riešenie, keď dva červené body môžu tvoriť uhlopriečku). Prípad, kedy dva vyznačené body tvoria uhlopriečku však môže mať rôzne podoby. Riešitelia najčastejšie ošetrili iba prípad, kedy rozdiel medzi x-ovými a y-ovými súradnicami je rovnaký, ale zabúdali na prípady, kedy je štvorec pootočený (z týchto prípadov je najľahšie viditeľný ten, keď sú dva červené body umiestnené vodorovne/zvislo a medzi nimi sa nachádza nepárny počet čiernych bodiek).