PALMA junior
Úloha o lúštení Korydoku

Autorské riešenie
[stiahni]

Úlohou bolo doplniť Korydoku rozmerov n x n tak, aby v každom riadku a každom stĺpci bolo každé z čísel od 1 po n práve raz, pričom jedno políčko Korydoku už máme vyplnené.

Myšlienkou nášho riešenia je, že ak neberieme do úvahy zadané číslo, vieme skonštruovať (nejaké) riešenie Korydoku. Potom stačí toto riešenie upraviť, aby vyhovovalo zadanej podmienke. To spravíme tak, že ku každému z čísel nášho vzorového riešenia pripočítame vhodné číslo, aby na správnom mieste vychádzalo správne číslo.

Najprv musíme nájsť spôsob, ako nájsť jedno "vzorové" riešenie: ako vyplniť tabuľku n x n číslami od 1 po n tak, aby sa v riadkoch ani stĺpcoch čísla neopakovali. To môžeme urobiť tak, že v každom políčku vypočítame súčet čísla riadka a čísla stĺpca. Keďže čísla riadkov rastú o jedna, máme zabezpečené, že v prvom stĺpci budú rôzne čísla. V druhom stĺpci budú tiež rôzne čísla a ešte k tomu posunuté o jedna, lebo narástlo číslo stĺpca, teda v jednotlivých riadkoch budú tiež rôzne čísla. Takto môžeme pokračovať ďalej a pre Korydoku rozmerov 4 x 4 dostaneme: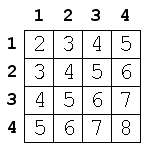

Lenže teraz sa v tabuľke vyskytujú čísla aj väčšie ako 4. Aby sme v tabuľke mali čísla iba menšie alebo rovné ako 4, ale zároveň nepokazili peknú vlastnosť, že v každom stĺpci sú čísla posunuté o jedna vzhľadom k predchádzajúcemu stĺpcu, každému z čísel určíme zvyšok pri delení 4. Zvyšok pri delení štyrmi však nadobúda hodnoty 0,1,2,3, ale my chceme čísla od 1 po 4, teda ku každému zvyšku ešte pripočítame číslo 1.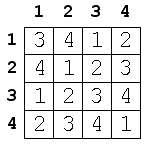

Všimnite si, že vlastnosť, že v každom stĺpci a v každom riadku sú rôzne čísla, ostala zachovaná len ak prekročíme hranicu číslo 4, tak začíname odznova od 1. Točíme sa teda v takejto štruktúre: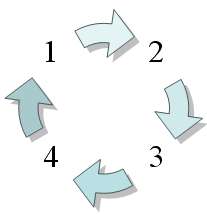

Vzorové Korydoku už máme. Teraz si ukážeme, ako ho upraviť tak, aby vyhovovalo zadanej podmienke. Nech napríklad chceme mať v 2. riadku a 3. stĺpci číslo 4. Keď sa pozrieme do nášho vzorového Korydoku, zistíme, že na príslušnom mieste je číslo 2.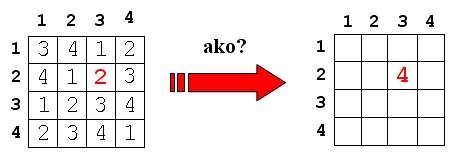

Vo vzorovom riešení máme v 2.riadku a 3.stĺpci číslo 2, ale my tam chceme mať číslo 4. Teda musíme k vzorovému číslu pričítať (4-2) = 2. Tak by sa ale pokazila vlastnosť celého Korydoku, preto musíme posunúť každé číslo tabuľky o 2. Aby sme však nedostali čísla väčšie ako 4, urobíme rovnakú fintu, ako predtým - vypočítame zvyšok po delení štyrmi a pričítame jednotku. Teda napríklad posunúť číslo 3 o 2 znamená urobiť z neho číslo 1. Pekne to vidieť na kruhovom šipkovom diagrame, ktorý je znázornený vyššie, každé číslo posunieme o dve šipky.

Výsledné Korydoku v našom prípade bude nasledovné: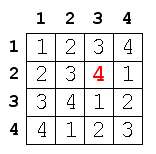

Riešenie úlohy môže vyzerať nasledovne:

Vaše zaujímavé riešenia a najčastejšie chyby

Úloha bola evidentne dosť náročná. O to viac oceňujeme riešenie aspoň dvoch poslaných riešení, ktoré boli relatívne funkčné a bodovo vyššie ohodnotené. Najčastejšou chybou bolo nesprávne chápanie číslovania tabuľky, ale za to sme body nesťahovali. Podľa zadania mal byť prvý riadok a stĺpec umiestnený vľavo hore. Odovzdané riešenia väčšinou riešili iba výpis čísla na príslušné miesto, ale celkové riešenie a výpis KoryDoku chýbalo. Vyplnené KoryDoku malo obsahovať čísla od 1 po N, v niektorých riešeniach sa dokonca objavili aj záporné čísla.