PALMA junior, Programovanie, ALgoritmy, MAtematika, súťaž pre mladých programátorov v Imagine

	PALMA junior

Úloha o ošetrení kapustných hláv

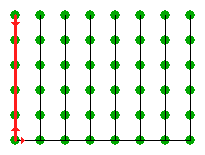
Autorské riešenie
[stiahni]

Existuje viacero spôsobov ako prejsť celým poľom. Jeden spôsob je postupne prechádzať stĺpcami zľava doprava a napokon sa vrátiť späť do ľavého dolného rohu poľa.

kapusty_neefektivne

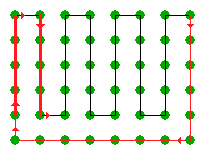
Počet kapúst na šírku je rovný hodnote v premennej stlpce a počet kapúst na výšku rovný hodnote v premennej riadky.

Počet prejdených krokov v jednom stĺpci tam a späť je rovný hodnote 2×(riadky-1). Počet krokov vo všetkých stĺpcoch tam a späť je rovný hodnote 2×(riadky-1)×stlpce. Počet krokov zľava doprava a späť je rovný hodnote 2×(stlpce-1. Celkový počet krokov je rovný hodnote 2×(riadky-1)×stlpce+2×(stlpce-1) = 2×riadky×stlpce-2.

Riešenie úlohy vychádzajúce z popísaného spôsobu môže vyzerať nasledovne:

viem kresli0
; v cykle tam a spat s posunom
  opakuj :stlpce-1 [
    do (:riadky-1)*:krok
    do -(:riadky-1)*:krok
    vp 90
    do :krok
    vl 90
  ]
  do (:riadky-1)*:krok
  do -(:riadky-1)*:krok

; navrat domov
  vl 90
  do (:stlpce-1)*:krok
  vp 90

; vypis
  ph
  vz :krok
  text "|Dĺžka cesty je rovná 2*riadky*stlpce-2 t. j.|
  vz :krok
  urobTu "vypis (zoznam "|stlpce * riadky:| :stlpce "|*| :riadky "| Dĺžka=| 2*:riadky*:stlpce-2 "|krokov|)
  text :vypis
  do 2*:krok
  pd
koniec

V predchadzajúci spôsobe riešenia sme prechádzali dvakrát po tej istej ceste. Na nasledovnom obrázku je ukázaný oveľa šikovnejší spôsob, ako prejsť všetkými kapustami tak, aby sme nemuseli prechádzať po tej istej ceste dvakrát.

kapusty_efektivne

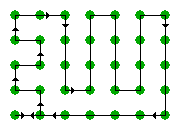
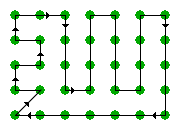
Každým krokom sa dostávame postupne od kapusty ku kapuste. Po 1. kroku sme prešli 1 kapustu, po 10. kroku sme prešli 10 kapúst atď. Celkový počet krokov na prejdenie celého poľa z ľavého dolného rohu a naspäť je rovný celkovému počtu kapúst t. j. hodnote riadky×stlpce.

Je možno vymyslieť iný postup, ktorý by bol ešte šikovnejší (efektívnejší) ako tento, v ktorom by sme použili menej krokov? Smelo môžeme povedať, že nie, lebo by sme neprešli všetky kapustami alebo by sme sa nevrátili na pôvodné miesto. Je to podobné akoby sme mali náhrdelník pozostavajúci z N korálikov, ktoré sú spojené N spojkami. Keby bolo počet spojok už len o jednu menej, tak sa nahrdelník roztrhne.

Najšikovnejšie (najefektívnejšie) riešenie problému (ku ktorému neexistuje efektívnejšie riešenie) nazývame optimálne riešenie.

Riešenie úlohy vychádzajúce z popísaného spôsobu môže vyzerať nasledovne:

viem kresli
; krok
  do :krok

; v cykle tam a spat s posunom
  urobtu "uhol 90
  opakuj :stlpce-1 [
    do (:riadky-2)*:krok
    vp :uhol
    do :krok
    vp :uhol
    urobtu "uhol 0-:uhol
  ]
  do (:riadky-1)*:krok

; krok a navrat domov
  urobtu "uhol 0-:uhol
  vp :uhol
  do (:stlpce-1)*:krok
  vp :uhol

; vypis
  ph
  vz :krok
  text "|Dĺžka cesty je rovná počtu kapustných hláv t. j.|
  vz :krok
  urobTu "vypis (zoznam :stlpce "|*| :riadky "|=| :stlpce*:riadky "|krokov|)
  text :vypis
  do 2*:krok
  pd
koniec

Poznámka:
Uvedené riešenie sa dá uplatniť pri riešení úlohy, v ktorej počet kapúst v riadku alebo stĺpci je párne číslo. Pri poli s celkovým nepárnym počtom kapúst by sme uvedený spôsob riešenia museli upraviť. Na nasledovných obrázkoch sú naznačené postupy ako prejsť polom s cekovo nepárnym počtom kapúst. V prvom prípade sa presúvame len vodorovne a zvisle, v druhom prípade sa pri jednom presune pohneme šikmo.

neparne_1.riesenie neparne_2.riesenie

Vaše zaujímavé riešenia a najčastejšie chyby

Úlohu riešilo 17 tímov. Takmer polovica riešení bola úplne správna. Niektorí ste si vďaka nepozornosti nevšimli v zápise úlohy, že sa treba vrátiť na pôvodné miesto, iní ste zabudli vypočítať a vypísať celkový počet prejdených krokov. V niektorých riešeniach ste použili menej efektívny spôsob tým, že ste predchádzali niektorými úsekmi dvakrát. Pri výpočte krokov ste niektorí používali pomocnú premennú, iní ste uviedli hodnotu riadky×stlpce. Väčšina súťažiacich namiesto zdôvodňovania efektívnosti riešenia opisovala postup riešenia úlohy.

PALMA junior

Úloha o ošetrení kapustných hláv