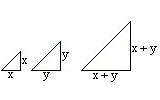PALMA junior, Programovanie, ALgoritmy, MAtematika, súťaž pre mladých programátorov v Imagine

	PALMA junior

Úloha o prekážkovej trati

Autorské riešenie
[stiahni]

Uvedieme iba jedno z mnohých riešení tejto úlohy. Zistíme dĺžku trate od štartu po cieľ bez ohľadu na prekážky - premenná celaDlzka. Spočítame výšky všetkých prekážok na trati - premenná celaVyska. Je možné si to predstaviť tak, že na trati dĺžky celaDlzka je iba jediná prekážka veľkosti celaVyska. Keďže korytnačka skáče pod uhlom 45 stupňou, pomocou Pytagorovej vety musíme vyrátať dĺžku skoku - odmocninu z dvoch vynásobíme premennou celaVyska. Výsledok získame tak, že od premennej celaDlzka odrátame dvojnásobok premennej celaVyska a pripočítame dvojnásobok skoku.

viem dlzka
ph
urobTu "celaDlzka 0
urobTu "celaVyska 0
kym [farbaBodu <> "cervena]
[
   do 1
   urobTu "celaDlzka :celaDlzka + 1
   ak farbaBodu = "modra
   [
    urobTu "vyska 0
    vl 90
    kym [farbaBodu = "modra]
    [
     do 1
     urobTu "vyska :vyska + 1
    ]
    vz :vyska
    vp 90
    do 1
    urobTu "celaDlzka :celaDlzka + 1
    urobTu "celaVyska :celaVyska + :vyska
   ]
]
(pis :celaDlzka - 2 * :celaVyska + 2 * :celaVyska * odmocnina 2)
koniec

Naozaj stačí Pytagorovu vetu použiť iba raz? Nemusíme dĺžku skoku počítať zvlášť pre každú prekážku? Preskúmajme nasledovný prípad:

Pytagorova veta

Prepona trojuholníka naľavo sa vypočíta ako súčin druhej odmocniny z čísla 2 a čísla x. Podobne sa určí prepona trojuholníka v strede. Je to súčin druhej odmocniny z 2 a čísla y. Prepona trojuholníka napravo je rovná súčinu druhej odmocniny z čísla 2 a x + y. Rovnaký výsledok však dostaneme, ak sčítame prepony prvých dvoch trojuholníkov.
Navyše, vzhľadom na to, že druhá odmocnina je v programe Imagine obmedzená na 5 desatinných miest, je vhodnejšie Pytagorovu vetu použiť iba raz na konci programu (ako v našom autorskom riešení). Pri použití Pytagorovej vety (a teda počítaní druhej odmocniny) pre každú prekážku zvlášť je riešenie úlohy menej presné. Celá procedúra by mohla vyzerať nasledovne:

Vaše zaujímavé riešenia a najčastejšie chyby

Mnohí zabúdali odrátať výšku prekážky od dĺžky trate. Niektorí nesprávne použili Pytagorovu vetu pri určovaní dĺžky skoku. Iní (pravdepodobne v dôsledku nedostatku času) pri počítaní dĺžky dráhy vôbec neuvažovali prekážky. Tím Nepoviem ako jediný rátal celkovú dĺžku a celkovú výšku prekážky, čím si zaslúžil našu pochvalu.

PALMA junior

Úloha o prekážkovej trati