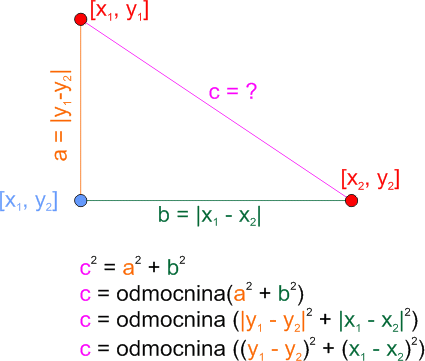PALMA junior, Programovanie, ALgoritmy, MAtematika, súťaž pre mladých programátorov v Imagine

	PALMA junior

Úloha o kory-voľbách

Autorské riešenie
[stiahni]

Pri riešení tejto úlohy budeme musieť vypočítať pre každú osadu súčet vzdialenosti z tejto osady do všetkých ostatných. Ústredná volebná komisia bude potom v tej osade, pre ktorú bude tento súčet najmenší.

V premennej suradnice sú uložené súradnice všetkých osád. Z týchto súradníc budeme počítať vzájomné vzdialenosti osád. Výhodné teda bude, ak si vytvoríme procedúru, ktorá nám vráti vzdialenosť dvoch súradníc, teda osád. Na výpočet vzdialenosti využijeme Pytagorovu vetu.

Samotná procedúra pre výpočet vzdialenosti môže vyzerať takto:

viem vzdialenost :o1 :o2
  vysledok odmocnina (
             ((posledny :o1) - (posledny :o2)) * ((posledny :o1) - (posledny :o2))
             +
             ((prvy :o1) - (prvy :o2)) * ((prvy :o1) - (prvy :o2))
           )
koniec

Parametre o1 a o2 obsahujú súradnice dvoch osád.

Pre každú osadu vypočítame súčet vzdialeností od tejto osady ku všetkým ostatným. Z týchto súčtov potom vyberieme osadu, ktorá mala súčet najmenší. Aby sme však mali s čím porovnávať získané súčty, vypočítame si súčet vzdialeností pre prvú osadu:

Pokračujeme vo výpočte súčtu vzdialeností pre ostatné osady. Výsledná procedúra môže vyzerať takto:

viem uvk
urobTu "minSuctuVzdialenosti 0

;zistime sucet vzdialenosti pre prvu osadu
urobTu "vybranaOsada prvy :suradnice
urobTu "suradniceUVK :vybranaOsada
prePrvky "osada :suradnice [
    urobTu "minSuctuVzdialenosti :minSuctuVzdialenosti + vzdialenost :vybranaOsada :osada
]

;zistujeme sucet vzdialenosti pre ostatne osady
prePrvky "vybranaOsada :suradnice [
    urobtu "sucetVzdialenosti 0
    prePrvky "osada :suradnice [
      urobtu "sucetVzdialenosti :sucetVzdialenosti + vzdialenost :vybranaOsada :osada
    ]

    ;ak najdeme mensi sucet, zapamatame si suradnice osady
    ak :minSuctuVzdialenosti > :sucetVzdialenosti [
      urobTu "minSuctuVzdialenosti :sucetVzdialenosti
      urobtu "suradniceUVK :vybranaOsada
    ]
]
pis slovo "|Najvhodnejšia osada pre ÚVK ma súradnice: | :suradniceUVK
koniec

Vaše zaujímavé riešenia a najčastejšie chyby

Zaujímavé riešenie objavil tím "vyssia-inteligencia Expert". Snažil sa nájsť osadu čo najbližšie k ťažisku týchto osád. Najčastejšou chybou bolo to, že ste začali porovnávať súčty vzdialeností s nejakým vopred určeným číslom. Ak by však najmenší súčet vzdialenosti bol väčší ako toto číslo, procedúra by nevrátila správny výsledok.

PALMA junior

Úloha o kory-voľbách