PALMA junior
Úloha o záchrane diváka

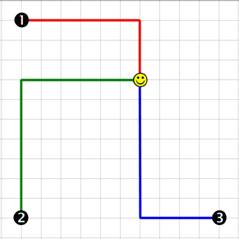
Autorské riešenie
[stiahni]

Najprv vypočítame vzdialenosti všetkých záchranárov od postihnutého diváka. Potom z týchto vzdialenosti nájdeme najkratšiu vzdialenosť a určíme záchranara.

Záchranári sa môžu pohybovať len vodorovne a zvislo, nie šikmo. Preto vzdialenosť medzi záchranárom a divákom vypočítame ako súčet dĺžky vodorovnej a zvislej časti cesty medzi záchranárom a divákom. Napr. vzdialenosť medzi prvým záchranárom na pozícii [x1,y1] a divákom na pozícii [xd,yd] vypočítame ako vzdialenosť(x1-xd)+vzdialenosť(y1-yd). Vzdialenosť je vždy nezáporné číslo. Je rovnaká aj pri vzájomnej zamene východzieho a koncového bodu na číselnej osi, napr. vzdialenosť(0-3)=vzdialenosť(3-0)=3. V programovacích jazykoch máme funkciu (operáciu) abs, pomocou ktorej vieme vypočítať vzdialenosť dvoch bodov na číselnej osi, napr. abs(3-0)=abs(0-3)=3. Potom dlžku cesty medzi 1.záchranárom a divákom vyjadríme v jazyku Logo výrazom (abs :x1 - :xd) + (abs :y1 - :xd). Podobne vyjadríme vzdialenosti medzi ostatnými záchranármi a uložíme ich do premenných dlzka1, dlzka2, dlzka3.

Druhou časťou riešenia je nájdenie najmenšieho čísla z trojice dlzka1, dlzka2, dlzka3. Urobíme to tak, že porovnáme prvú dvojicu a potom menšie číslo z tejto dvojice porovnáme s tretím číslom.

Výsledný príkaz výpočet vyzerá nasledovne:

Uvedené riešenie v prípade rovnosti najkratších vzdialenosti vypíše len poradové číslo jedného záchranára. Pre danú situáciu by toto riešenie mohlo byť postačujúce.

Iné riešenie tejto úlohy využíva zoznamy na uloženie zadaných pozícií záchranárov a diváka, výpočítané dĺžky a tiež na zaznamenanie záchranárov vyhovujúcich zadaniam úlohy.

Vedeli by ste vyriešiť zadanú úlohu pre ľubovoľný počet záchranárov?

Pozor pri používaní zátvoriek, správne má byť uvedené (abs :x1 - :xd) + (abs :y1 - :xd). Výraz abs (:x1 - :xd) + abs (:y1 - :xd) sa vyhodnotí abs s výrazom (:x1 - :xd) + abs (:y1 - :xd), čo je nesprávny výsledok.

Touto úlohou sme chceli dosiahnúť, aby ste si precvičili prácu s premennými, používanie parametrov v procedúre, používanie príkazu vetvenia. Ďalej sme chceli, aby ste prišli na algoritmus výpočtu vzdialenosti medzi pozíciami v pravouhlom hľadisku a výpočet najmenšej hodnoty z troch čísel.

Do riešenia tejto úlohy sa pustilo 9 tímov. Páčili sa nám riešenie tímu Baša a Saša Expert a riešenie Bali Michala. V svojich riešeniach boli dôslední a uvádzali aj prípad, keď došlo k rovnosti 2 a 3 najmenších dlžok.

Najčastejšie nedostatky, ktorých ste sa dopustili vo svojich riešeniach:

• pri výpočte vzdialenosti ste sčítovali rozdiely súradníc, a nie súčet vodorovnej a zvsilej vzdialenosti, takto ste mohli dosťať aj záporné vzdialenosti, čo je nezmysel,
• neošetrenie prípadu rovnosti vzdialenosti s tým, že nevypísalo číslo žiadneho záchranára, čo by vb realite vyzeralo tak, že keď majú dvaja záchranári rovnako blízko k postihnutému, že napokon k nemu nepríde žiaden záchranár,
• namiesto príkazu priradenia s rozdielom dvoch čísel, bol použitý cyklus s odčítaním čísla 1 od daného čísla
• v niektorých riešeniach ste uvádzali viacero príkazov ak, pričom ste mohli použiť niekoľko príkazov ak2 buď vnorením do seba alebo použitím spojky zaroveň.
• pre prácu s pomocnými premennými, ktorých hodnotu nepotrebujem vedieť v inej procedúre odporúčame použiť príkaz priradenia urobTu namiesto príkazu urob,
• niektoré riešenia boli iba riešeniami ilustratívneho príkladu zo zadania, nie všeobecným riešením pre ľubovoľné pozície troch záchranárov a diváka.