 |
|
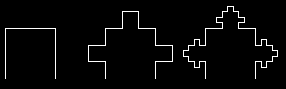 |
|
 |
|
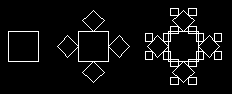 |
|
 |
|
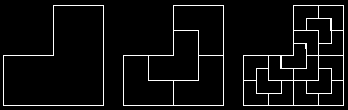
|
|
 |
|
 |
|
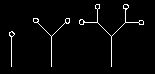 |
|
 |
|
|
|
 

|
|
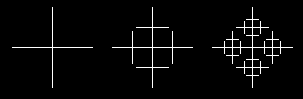 |
|
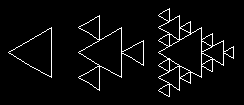 |
|
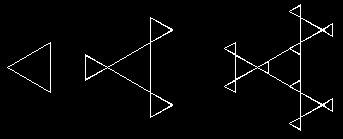 |
|
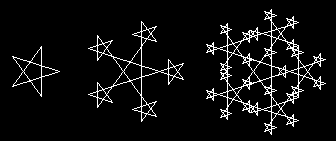 |
|
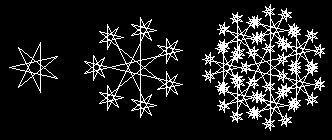 |
|
 |
|
 |
|

|
|
 . . .
. . . 
|
|
 . . .
. . .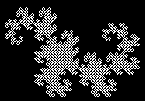
|
|
 . . .
. . . 
|
|
 |
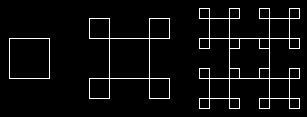
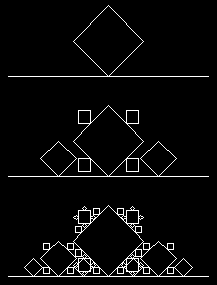
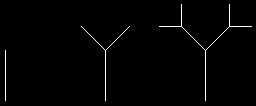
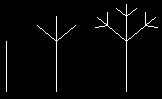
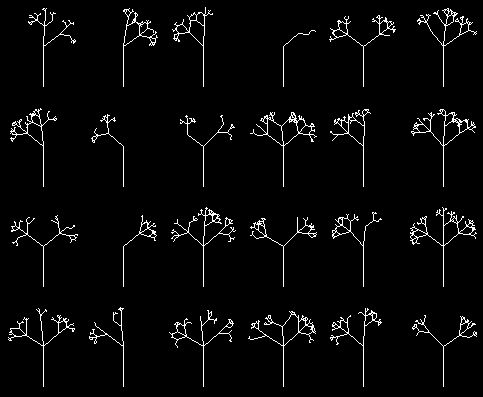
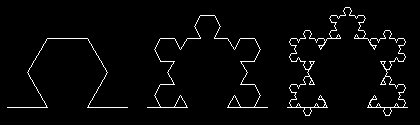
Rekurzívne krivky.
 |
|
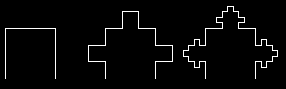 |
|
 |
|
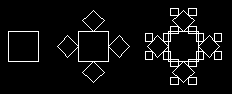 |
|
 |
|
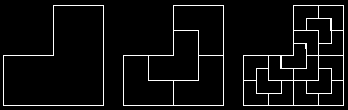
|
|
 |
|
 |
|
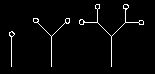 |
|
 |
|

|
|
 

|
|
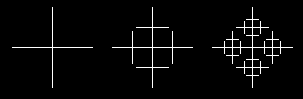 |
|
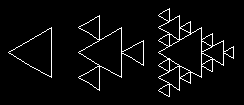 |
|
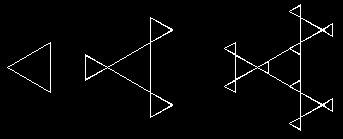 |
|
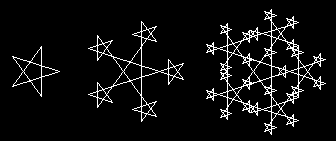 |
|
 |
|
 |
|
 |
|

|
|
 . . .
. . . 
|
|
 . . .
. . .
|
|
 . . .
. . . 
|
|
 |
Backtracking
10 10 2 2 9 9
XXXXXXXXXX
X.......XX
X.XX.XX.XX
X.XX.XX...
X.XX.XXXXX
X.XX.XXXXX
X.XX.XXXXX
X......XXX
X.XXXX...X
XXXXXX.XXX
Testovací súbor s bludiskom si môžete stiahnuť tu: bludisko.dat.Rekurzívne triedenie